前置知识:向量,三角函数,线性代数
如果你处于1.4版本以上,请将下文中的projectile均换成Projecttile(大小写)
Hi,要不要来多人运动?咳,我说的是这个
好啦言归正传,本篇教程主要想讲的就是跟游戏内物体运动(Movement)有关的,至于是不是多人就不好说了。总体来说,一个物体的AI可以分为决策和行动两个部分,对于泰拉瑞亚来说,行动部分又可以分为攻击和移动,但是两者又可以混在一起说,毕竟不论怎么攻击都需要移动的嘛。所以移动(运动)可谓是AI编写中最绕不开的部分了,只有写好移动才能构造出想要的AI效果。
但是物体运动这方面内容真的非常多,之前写过的追踪只能算是其中一个很小的部分,如果要把这部分讲完都可以出一本书了。所以本篇教程我只会挑一些泰拉瑞亚里面经常使用的移动算法以及其原理进行讲解,同时,我还希望大家能够对位置、速度、加速度有一个明确的认识,以后代码中会大量运用这些概念。
基本概念
位置(Position)比较好理解,在泰拉瑞亚中,我们用二维坐标 \((x,y)\) 表示一个物体的位置。
物体运动最基本的属性就是速度(Velocity),但是我们一定要注意区分一个概念,速度向量(Velocity)和速度大小(Speed)。我们日常生活中所说的速度通常都是指speed,但是speed只是速度向量velocity的一个属性,所以我们并没有办法通过speed去描述整个运动过程。但是如果我们使用速度向量,假设一个物体当前的速度向量为 \(\vec{v}\),位置为 \(\vec{p}\) ,那么下一帧我们就可以计算出所处位置为 \(\vec{p}+\vec{v}\)。所以速度表示的就是单位时间位置的变化。
加速度( Acceleration )其实就是单位时间速度的变化量,比如上一帧我们速度是 \(\vec{v}\),这一帧我们速度增加了 \(\vec{a}\),那么这一帧的速度就变成了 \(\vec{v}+\vec{a}\),那么问题来了,这一帧的位置会怎么变呢?
要理解这个问题我们先假设运动都发生在X轴正半轴上,并且速度方向都是朝着X轴正方向行进
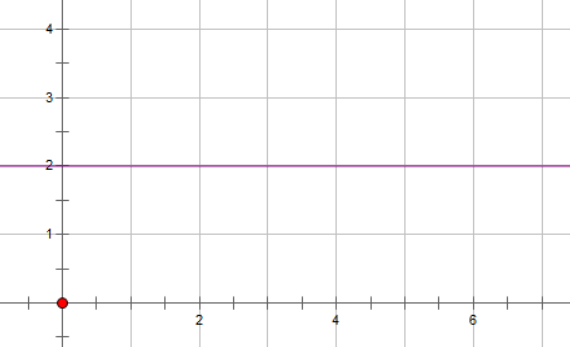
假设我们初始速度为0,位置在0点,加速度为2,那么我们可以画一个加速度随时间变化的图像,我们管加速度的这个函数叫做 \(a(t)\)
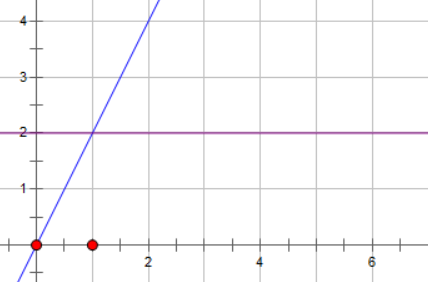
可以看到,加速度在任何时刻都是2,那么此时速度变化的图像应该是这样的,蓝色的一条线,我们叫做 \(v(t)\)
我们可以看到时刻1速度大小变成了2,时刻2,速度大小变成了4,这也符合我们之前所说的加速度的定义。但是要注意,时间是连续的,所以在时刻1.5的时候,速度是3,时刻1.25的时候,速度是2.5。你有没有发现什么?在时刻 \(t\),我们的速度大小是 \(2t\),对不对?
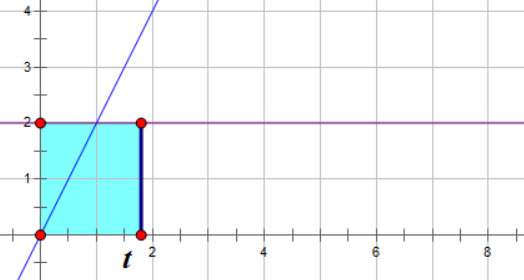
那么我们再来看看这个 \(2t\),它其实可以看做是从加速度图像到x轴上的这一段区域的面积,因为加速度的函数图像是 \(a(t) = 2\),所以这一段面积就是 \(2t\)
所以我们可以推断,速度对位置的影响应该也是等于函数与X轴正半轴的投影面积是相等的,事实也的确如此。
绿色的线就是位置与时间的关系了,我们可以从图中轻易验证,绿色线的Y坐标值就等于蓝色线下面的投影面积值,比如时刻2,三角形面积是\(\frac{1}{2} (2\times 4)=4\)。
总结一下,由此我们可以推出一个更一般化的规律,假设加速度为 \(a\),则速度的变化是 \(v=v_0+at\),其中 \(v_0\) 是初始速度。位置的变化就是 \(p_0+\frac{1}{2}vt\),展开来就是 \(p_0+\frac{1}{2}(v_0t+at^2)\)。
如果你学过物理,应该对上面的这些推导和公式很熟悉了。其实这个函数投影到X轴正半轴的阴影面积就是数学中的积分(Integration),速度对位置的贡献我们还可以写成 \[\int_{0}^{t} v(t) dt=p(t)+p_0\]
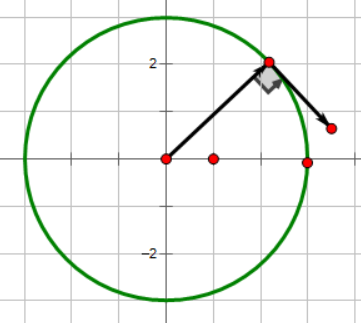
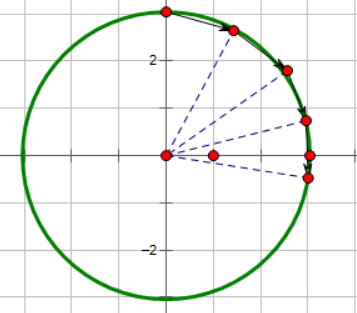
但是泰拉瑞亚是个二维世界,所以只考虑一维的情况是不够的,那么对于二维向量的速度和位置关系,我们只需要把每个维度的函数分别积分就能得到最终的位置二维坐标了。具体来说,假设有一个物体速度随时间变化函数为 \((cos(2t), sin(3t))\),那么它的位置与时间关系就是 \((sin(2t)/2, -cos(3t)/3)\),如果我们把它的轨迹在TR中画出来:
这里提供一下代码:
float t = (float)Main.time * 0.1f; // 生成火焰粒子 var dust = Dust.NewDustDirect(player.position, 1, 1, MyDustId.Fire, 0, 0, 100, Color.White, 2f); dust.noGravity = true; dust.velocity *= 0; dust.position = player.Center + new Vector2((float)Math.Sin(2 * t) / 2f, -(float)Math.Cos(3 * t) / 3f) * 100f;
这种 \((f(t), g(t))\) 来描述运动轨迹的方法也是非常重要的,事实上,它在数学中叫做参数方程(Parametric Equation)。我们能用参数方程实现很多优美的轨迹,最简单的画圆的参数方程就是 \((cos(t), sin(t))\) 。
既然有从速度推出位置的方法,那自然也有从位置变化推断出速度的方法,如果时间是连续的,我们就需要对位置变化函数进行求导(微分),求导的方法我这里就不多做介绍了。不过如果时间不是连续的,比如泰拉瑞亚,以及各种游戏,每秒只能执行60帧,所以速度的变化就可以近似成每帧位置与上一帧的差,这个思想非常重要。具体的应用我们以后会讲到,现在我们要知道的是,速度、加速度和位置,是可以互相转化和推导的。
角速度/加速度也是一个常用的概念,其实就是向量弧度的变化,比如我们在三角函数基础那一章提到的方法,就是通过改变向量的角速度来实现诡异曲线的,但是角速度与运动轨迹的映射并不简单,因为原先的二维速度函数 \((x(t), y(t))\) 会变成这样\[(x(t)\cos\theta(t)-y(t)\sin\theta(t), x(t)\sin\theta(t)+y(t)\cos\theta(t))\]
不要问我这个东西怎么算,我不想算QAQ。所以单纯用角速度去实现某个轨迹显然不是个好主意,因为角速度产生的轨迹很难预测。
那么以上就是运动系统的一些基本概念,接下来我们就介绍几种典型的运动模式,来运用以上概念。
运动模型
圆周运动
如果有学过物理,那么你一定会对圆周运动公式 \[F = \frac{mv^2}{r}, F=mω^2r \]
比较熟悉,同时根据牛顿第二定律 \(F=ma\) ,你可以把上面的公式转化为 \(a=\frac{v^2}{r}, a = ω^2r\),也就是说,你得到了一个向心加速度的公式。
因为是向心加速度,所以方向一定是朝着圆心的,于是我们可以得到这个一个加速度向量,那么我们试试放在游戏里效果如何吧?
var player = Main.player[projectile.owner]; // 半径r = 100,线速度v = 10 var unit = (player.Center - projectile.Center).SafeNormalize(Vector2.Zero) * 10 * 10 / 100f; projectile.velocity += unit;
我们会发现轨迹其实不是个正圆,而且玩家只要稍微一移动,整个轨迹就会乱套。这是因为圆周运动其实是模拟的重力,并且这是个稳定形态,一旦玩家位置或者弹幕速度发生一点变化,只靠加速度是无法还原稳定形态的。我们回看一下位置的函数 \(p_0+\frac{1}{2}(v_0t+at^2)\) ,所以轨迹不止是由加速度决定的。这种写法用来实现一些简单的环绕还是不错的,之后会讲到。
那么我们可以做第二次尝试,这次我们只用速度,忽略掉加速度产生的任何影响。
由于速度在任何时候都是和圆周相切的所以可以利用向量旋转直接求
但是你可能会发现,这时候初始位置 \(p_0\) 又会影响轨迹,只要玩家稍微移动一下,轨迹还是不对。就算是玩家不会动,因为游戏每秒只有60帧,所以可能会让某些点的速度偏离准确的轨迹,每帧偏离一点点,几秒后弹幕就会偏离一大截。所以这个方法也不行。(补充阅读:显式欧拉法)
另外一种方法是隐式欧拉法,我们先把下一帧应该在的位置计算出来,让弹幕往那个方向运动,或者只修改弹幕的位置,这时候就用上参数方程 \(cos(t), sin(t)\),其中从 \((0, 2\pi)\) 会刚好旋转一周,代码如下:
// 旋转点速率可以自行调整 var t = Main.time * 0.1f; var player = Main.player[projectile.owner]; // 要把弹幕速度归零,否则圆会有一个位移 projectile.velocity = Vector2.Zero; // 半径r = 50,以玩家中心为圆心 projectile.Center = player.Center + new Vector2((float)Math.Cos(t), (float)Math.Sin(t)) * 50f;
但是你可能会说,如果只用位置而忽略速度会不会导致很多与速度有关的信息丢失啊(比如旋转方向,碰撞检测)?为了解决这个问题,我们就要用到一个取巧的方法:追及目标点。
我们之前是直接把位置暴力设为了圆的位置,但是实际上我们大可不必那么暴力,而是用较快的速度追击目标位置,具体来说,可以这么写:
// 旋转点速率可以自行调整 float t = (float)Main.time * 0.1f; var player = Main.player[projectile.owner]; // 目标位置(我偷个懒 var targetPos = player.Center + t.ToRotationVector2() * 50f; projectile.velocity = (targetPos - projectile.Center) * 0.3f;
这样我们的速度也有了,还会在玩家移动的时候追击。如果不希望有追击我们也可以把*0.3f去掉(这样就是立即追上)。当然如果需要追击再明显一点也可以把这段改成追踪算法。这种方法是目前最有效的圆周运动写法。
当然,除了追及,还可以直接利用这一帧和上一帧的位置差作为速度,这只是单纯的为了旋转角度等额外功能,这个速度并不参与真正的运动。
如果你想要的是椭圆运动,可以用椭圆公式 \(acos(t), bsin(t)\),如果在此基础上还要旋转椭圆,我们可以直接旋转向量,就像这样:
// 旋转点速率可以自行调整 float t = (float)Main.time * 0.1f; var player = Main.player[projectile.owner]; // 目标位置,宽2,高5的椭圆 + 顺时针旋转45度角 var targetPos = player.Center + new Vector2(2 * (float)Math.Cos(t), 5 * (float)Math.Sin(t)).RotatedBy(0.785f) * 50f; projectile.velocity = (targetPos - projectile.Center);
模拟圆周运动这个部分提醒我们,在游戏开发领域,有时候太过数学化会使问题变得过于复杂,而且因为游戏帧率有限,结果可能不准确,所以我们需要用更好的方法去模拟这个运动模型。除了显式隐式欧拉法以外,我们还有 Verlet 积分法和 Runge-Kutta 4 法去更精准的拟合这个运动模型,感兴趣的话可以去了解一下,教程里只会涉及隐式欧拉法。
渐进运动
追踪
最简单的追踪运动当然就是直接朝着目标运动啦,正如我在旧版追踪教程中讲的那样,这样做的缺点是渐变非常生硬。在这里还是提供一下代码:
projectile.velocity = Vector2.Normalize(targetPos - projectile.Center) * 10f;
旧版教程讲的第二种追踪方法就是速度渐变法,通过当前和目标速度进行加权平均从而比较柔和的接近目标,缺点是在碰撞体积比较小的情况下容易围着目标点转圈从而导致打不中。代码如下:
// 目标速度 var targetVel = Vector2.Normalize(targetPos - projectile.Center) * 10f; // 加权平均 1份目标速度和10份当前速度 projectile.velocity = (targetVel + projectile.velocity * 10) / 11f;
加权参数对弹幕轨迹的影响是需要考虑的,目标速度的权值越大,追踪路线就越准确,轨迹就越生硬,反之轨迹就越柔和。于是旧版教程我还提出了一个动态权值的算法,根据离目标的距离改变加权参数,达到轨迹既柔和又准确。除此之外,你还可以弹增加幕extraupdates,一帧多更新几次位置,也能达到相似的效果。
如果需要让物体远离目标,那么只需要把目标速度反向即可,同时注意处理好边界,毕竟如果超过一定范围还要原理就有点不符合逻辑。
修改角速度当然也能实现跟踪,实现方法就是对速度的角度和目标角度进行加权平均,但是由于角度是有周期性的所以并不是很好进行平均:
var targetPos = (target == null) ? Vector2.Zero : target.Center; float targetR = (targetPos - projectile.Center).ToRotation(); float selfR = projectile.velocity.ToRotation(); float dif = MathHelper.WrapAngle(targetR - selfR); float r = selfR + dif * 0.3f; projectile.velocity = projectile.velocity.Length() * r.ToRotationVector2();
追踪效果一般,很容易绕圈,但是轨迹看上去还不错。
除此之外,追踪也可以用修改位置的方法实现。但是由于少了速度带来的不确定性,这种实现方法更应该说成是渐进。基本操作就是把自身位置和目标位置做加权平均,是不是很暴力?如果这么做那么渐进的速度会是指数级的,但是在渐进的最后几帧位置变化会很少,会出现一个平缓的过程,很多游戏的平滑相机其实就是用这类算法实现的。
代码如下:
// 需要移动到的位置,加权平均 var pos = 0.9f * projectile.Center + 0.1f * targetPos; // 然后假装自己是用速度实现的 projectile.velocity = pos - projectile.Center;
当然,单纯利用速度也可以这么写:
var targetVel = (targetPos - projectile.Center) / 10f; projectile.velocity = targetVel;
同样也是越靠近目标速度越慢。那么问题又来了,如果我不想要指数级靠近,而是想自己定义靠近目标的速度怎么办呢,那么我们就可以使用插值了。我们要注意的是,由于插值不好随意重置,所以使用插值函数最好保证插值完全描述一个运动过程,追踪其实就不好用插值,因为目标有可能动来动去。对于固定轨迹,插值就会显现出巨大的威力:
这张图的效果就是用Sin的插值+速度渐进实现的,代码如下
float t = (180 - projectile.timeLeft) / 180f; var player = Main.player[projectile.owner]; // 先求出法向量,然后法向量的长度由sin决定 var normal = Vector2.Normalize((player.Center - _startPos).RotatedBy(1.57f)) * (float)Math.Sin(t * 6.28f) * 50f; // 这是应该被设置的位置 var pos = _startPos * (1 - t) + player.Center * t + normal; // 渐进这个位置 projectile.velocity = (pos - projectile.Center) * 0.1f;
其中_startPos是我记录的弹幕初始位置。
最后我们当然要想想如何用加速度来实现追踪,其实这个方法在泰拉瑞亚里面应用的挺广泛的,因为如果boss和小怪追你都用前面几种方法,你还能有全尸吗?
于是我们可以先计算出目标速度,然后用加速度渐进这个速度,这次我们选用速度向量的两个分量分别渐进:
// 目标速度 Vector2 targetVel = Vector2.Normalize(targetPos - projectile.Center); targetVel *= 7f; // X分量的加速度 float accX = 0.2f; // Y分量的加速度 float accY = 0.1f; projectile.velocity.X += (projectile.velocity.X < targetVel.X ? 1 : -1) * accX; projectile.velocity.Y += (projectile.velocity.Y < targetVel.Y ? 1 : -1) * accY;
这个方法的好处也是缺点就是很容易overshoot,也就是俗称刹不住车,而且转向很不灵活,但是这正好符合怪物和召唤物的ai,不然玩家就难受了。效果如图:
这种方法还有个好处,就是可以打AOE。
冲刺
对于怪物AI,还有一种常见的攻击方式就是冲刺。冲刺行为分为两个阶段,准备阶段和冲刺途中阶段。准备阶段用于确定冲刺方向,距离等信息,然后冲刺阶段只对目标位置进行运动,这样做就是为了防止出现追踪玩家的情况。实现起来可以使用状态机,或者简易版状态机。
代码也很简单,这里的角度变化我用的也是渐进,但是冲刺过程用的是插值+计算速度:
private enum AttackState : int {
Ready,
Dash,
};
private AttackState State {
get { return (AttackState)(int)projectile.ai[0]; }
set { projectile.ai[0] = (int)value; }
}
private int Timer {
get { return (int)projectile.ai[1]; }
set { projectile.ai[1] = value; }
}
// 目标冲刺位置
private Vector2 _targetPos;
// 冲刺起始位置
private Vector2 _startPos;
public override void AI() {
switch (State) {
case AttackState.Ready: {
projectile.velocity = Vector2.Zero;
// 找最近的怪物
var target = ProjUtils.FindNearestEnemy(projectile.Center, 800);
if (target != null) {
Timer++;
var diff = (target.Center - projectile.Center).ToRotation();
if (Timer == 60) {
// 确定冲刺起始位置和结束位置
projectile.rotation = diff;
_targetPos = projectile.Center + Vector2.Normalize(target.Center - projectile.Center) * 500f;
_startPos = projectile.Center;
State = AttackState.Dash;
Timer = 0;
} else {
// 渐进旋转角
projectile.rotation = projectile.rotation + MathHelper.WrapAngle(diff - projectile.rotation) * 0.1f;
}
}
}
break;
case AttackState.Dash: {
// 冲刺过程就是单纯的冲,这里用的是位置渐进
var factor = Timer / 30f;
var pos = _startPos + (_targetPos - _startPos) * factor;
projectile.velocity = pos - projectile.Center;
Timer++;
if (Timer == 30f) {
State = AttackState.Ready;
Timer = 0;
}
}
break;
default:
break;
}
}
冲刺的运动过程可以把之前讲过的方法融合在一起,这部分的写法其实很自由。
其他运动
游荡
在弹幕或者NPC无法锁定或者攻击到目标的时候,除了让它静止不动以外,还可以选择让它随机游荡。随机游荡这件事实现的时候需要注意,如果你只是给物体一个随机速度肯定是行不通的,绝大部分情况下只会让物体在原地鬼畜。(虽然可以用一些光滑随机函数,比如Perlin噪声,去实现平滑的运动过程,但是CPU开销比较大)。
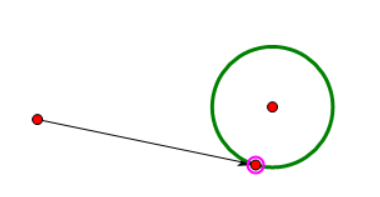
那么这里我有一个利用速度变化实现游荡的方法:追圆法(不知道学界有没有定义过,反正我这里先这么叫)。
原理很简单,我们在物体的正前方放一个看不见的圆,圆上有一个看不见的点,我们让物体每帧都朝这个看不见的点上面运动
由于圆上的点很好求,我们只需要知道它的弧度,那么对这个弧度进行操作就可以改变圆上点的位置。这时候我们就不需要一个光滑的随机函数了,因为圆上点的随机变化被映射到物体速度上的时候已经很光滑了。于是我们可以这么写:
// 圆心位置 var center = projectile.Center + projectile.velocity * 3; // 角度随机增加变化 rad += Main.rand.NextFloatDirection() * 0.5f; // 半径50,圆上的点 var pos = center + rad.ToRotationVector2() * 50; projectile.velocity = Vector2.Normalize(pos - projectile.Center) * 10f; projectile.rotation = projectile.velocity.ToRotation();
当然,这个方法不同的圆位置,半径大小,随机偏移速度大小,都会造成不同的游荡运动风格,具体如何大家可以自行探索,这个东西的自由度高的离谱。还有就是如果你觉得这个方法的速度变化还是太大了,可以结合之前所学的渐进方法让速度变化变得柔和。从这个方法你或许可以感觉到,想要让生硬的线条变得平滑,需要进行怎么样的操作。
总结
对于实时游戏来说,如果对轨迹准确度要求比较高的情况下,一定要通过位置来进行移动,除此之外,如果修改位置能达到要求,还是尽量使用位置修改。当然,如果你本身就想让轨迹变得杂乱无章,用速度和加速度也是不错的选择。












啊这,在写了,在写了
学会了
学会了。谢谢
如果想让很多个不同位置弹幕围绕一个中心旋转应该怎么办,试了一下追击目标点的代码后我的所有生成的弹幕都跑到一块去再旋转了
那就追击圆上不同的点呗,每个弹幕都在计时器算出来的位置基础上加个弧度偏移