本篇教程不像个教程,更像是随手写的博客文章。不过目的都是一样的,就是向你们科普一些计算机领域的知识。至于它如何被应用到泰拉瑞亚里,很难说,不过了解它有助于以后的代码编写。
为什么是二进制?
现代计算机通常都用二进制来表示数据(别说量子,咱不懂),也就是说,对于计算机中数据的最小单元,不是1就是0。为什么人类都是使用十进制而计算机只能使用二进制呢?这要从计算机底层的电路开始谈起,现实世界中可没有什么非0即1的东西,就像绝大部分事物并非非黑即白一样,而是精致的灰。电路也是如此,电压不可能在时间 \(t\) 之前是0V,在时间 \(t\) 那一瞬间变成5V。从0V到5V必将是一个连续的过程,慢慢的增长电压,不管它是不是线性的变化。整个过程也必然会花费一定的时间,即使这个时间小到人难以察觉。
如果我们想要表示一些信息,那么根据电压的大小来表示会是一个不错的选择,如果电压比较大,我们就认为它代表的信息是1,否则就是0。那么问题来了,我们为什么一定要表示成1或者0,根据电压大小0V代表0,1V代表1,5V代表5不行吗。当然可以,但是问题在于,如果把电压按照这种方式分段,抗干扰能力就会急剧下滑。为什么会这样呢?我们知道电子元件两端的电压大小是可以通过调节电阻来改变的,如果想要接近0V的电压我们只需要把电路也设为接近0的数,如果想要增加电压我们就可以增加电阻的大小。但是这个变化不是线性的,如果想要精准的确定某个电压我们需要计算(假设串联两个电阻 \(R_1, R_2\))
\[ U_1 = \frac{U}{R_1+R_2}R_1 \]
解得
\[ R_1 = \frac{U_1R_2}{U-U_1} \]
画出图来是这样的
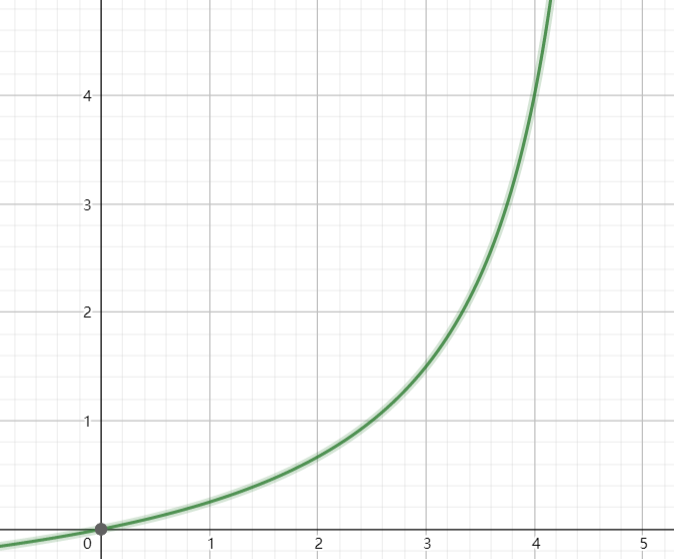
可以看到,如果你想要区分1V电压和2V电压,那么他们之间的电阻大小的变化可能很小,此时我们还要考虑一个问题,就是电子元件自身是会发热的,如果发热了,电阻会随着温度变化。现在再来考虑电压分段的问题,如果发热以后电阻从2滑到了1,那么原先表示的数字就不对了。我们还可以求出电路发热功率的函数:
\[ P = I^2R = (\frac{U}{R_1+R_2})^2 R_1 \]
以及其图像,我们可以看到电阻比较小(却又不接近0)的时候就是发热最严重的地方,而这段区间根据上图可以跨越好几个电压层级,那么此时电压是不是特别不稳定?而随着电阻的增大,发热会减小,所以电阻越大或者越接近0,电压就越稳定。
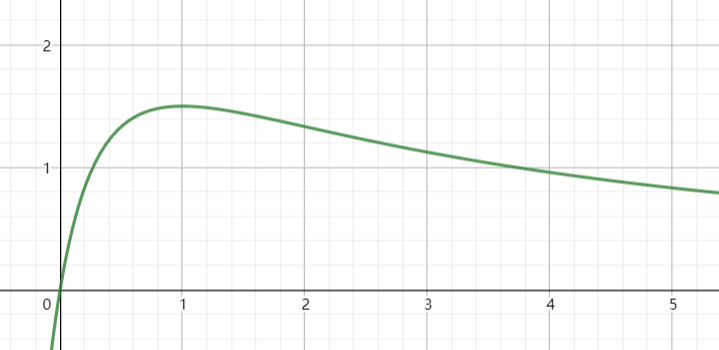
综上所述,为了保持稳定性和阻止电子元件过热,电压要么0要么很高是比较好的选择,否则就极其脆弱。而这种非0即1的设定正好跟二进制表示相符,这就是为什么现代计算机通常都使用二进制。不过即使是二进制,也会出现不稳定的问题,有兴趣可以去了解一下内存条中ECC之类的纠正机制,内存中有些比特位甚至会自己翻转什么的,不过比起其他进制,二进制要好太多了。
二进制编码
我们知道了一个基本单元的值要么是0要么是1,那么0和1是如何表示各种各样的数据的呢?0和1本身没有什么意义,他们的意义是我们程序员赋予的。对于内存中的一串01串,我们有各种各样的编码规则去解释他们,本文我们就着重讨论一下整数和浮点数的表示。
无符号整数编码
对于任何一个十进制自然数,我们都可以把它解释成一个二进制数,接下来我会用 \((114514)_{10}\) 这样的标记来表示十进制数 114514,如果是二进制就是 \((1 1011 1111 0101 0010)_{2}\) 这样的标记。所以说 \((114514)_{10}\) 转化为二进制就是 \((1 1011 1111 0101 0010)_{2}\) 。二进制的转化非常简单,10进制数 \((114514)_{10}\) 就等于
\[4+1\times10+5\times100 + 4\times1000 + 1\times 10000 + 1\times 100000\]
或者
\[4\times10^0+1\times10^1+5\times10^2 + 4\times10^3 + 1\times 10^4 + 1\times 10^5\]
发现规律没有?而二进制数也是一个道理,假设我有一个数 \((1101)_{2}\),那么它代表的十进制数其实就是
\[(1101)_{2} = 1\times2^0 + 0\times2^1 + 1\times2^2 + 1\times2^3 = 1 + 4 + 8 = (13)_{10} \]
进制之间的转换也是很简单,还是从十进制推导一下,\((114514)_{10}\) 的每一位是怎么求出来的呢?首先我们把 \((114514)_{10}\) 模10,得到4,那么4就是最低的十进制位。然后我们把这个值除以10(向下取整),得到 \((11451)_{10}\),同样的模10,得到1,作为下一位,然后除以10,依次类推,直到这个值变成0。对于任意进制伪代码大概如下:
// x是要被转化的数字,base是进制数
function ChangeBase(int x, int base){
while(x != 0){
倒着输出( x % base );
x /= base;
}
}
十进制转二进制也就是把数拆成2的次方的和,具体做法就是不断模2,然后除以2。
计算机中的无符号整数就是用的二进制进行编码,不过计算机中二进制位不是无限的。CPU在对二进制数进行操作的时候,从来都不是一个位一个位的计算的,通常我们会把二进制数进行分组,以组为单位进行计算。最小的一组由8个二进制位组成,叫做一个字节(byte)。32位CPU一次操作的数据是由32个二进制位组成,也就是4个字节,通常也叫做双字(double word)。而64位CPU支持64个位组成的8个字节的组,也叫做四字(quad word)。除此之外两个字节也可以拼起来组成一个组,也叫做字(word)。 这就是32位CPU和64位CPU的区别之一,64位CPU一次能同时处理的信息比32位CPU多。
对应到编程语言中的数据类型,byte在C#里真就叫byte,而两个byte组成的长度为16位的数据结构在C#里叫short,4个byte组成的32位的整数在C#里是int,8个byte组成的64位的整数在C#里叫long。
上述的数据类型除了byte都是带符号的数据类型,也就是说除了能表示正数以外,还可以表示负数,而byte是无符号类型,只能表示非负整数。我们暂时先不考虑负数,对于一个32位的无符号整数类型,32个二进制位能表示的范围就是从32个0一直到32个1。32个0很显然是0,32个1就是
\[2^0+2^1+2^2+\dots+2^{31} = 2^{32}-1 = 4294967295\]
所以32位无符号整数(unsigned int)能表示的范围就是 0 ~ 4294967295。
那么byte,无符号的short类型,无符号的long类型所能表示的范围应该是多大?
带符号整数编码
对于你们来说,可能更熟悉另一个范围,也就是带符号的int的范围: -2147483648 ~ 2147483647。为什么带符号以后的32位数范围看起来这么奇怪呢?为什么负数值域比正数会多一个呢?
假设我们来设计带符号整数的编码,我们可能会这么设计:让最高的一个位代表正负,之后的其他位负责表示值。那么 \((-7)_{10}\) 在4位二进制数中就会被表示为
\[ (-7)_{10} = (1111)_{2} = -(2^0+2^1+2^2) = -(1+2+4) \]
看上去不错,对吧?但是这种表示方法有一个巨大的问题,就是如何表示0?以下两种方法都能表示0
\[ (0000)_{2} = +0, {1000}_{2} = -0 \]
那么此时我们就有了一个正0和一个负0,但是这显然没有意义,对于整数我们根本不需要区分0是正还是负,这么做我们的表示方法就出现冗余了。更致命的是,如果按位比较,\(0000\) 是不等于 \(1000\) 的,也就是说0不等于0,那么显然有逻辑错误。还有一个问题,就是做算数的时候,比如减法,我们就得特殊处理最高位。根据减数和被减数最高位的不同总共有4种情况,之前的二进制加法只要根据运算去设计电路就行了,而到了最高位却得单独处理,整个运算方式都会改变,这无疑给电路的设计和运行速度增加了挑战。 比如,从0开始减去1现在变成了翻转位然后加一。
目前最流行的编码方式是一种叫做 Two’s-Complement(中文应该叫啥啊QAQ)的编码方式,相比于我们之前的想法,它只是把最高位所表示的2的次方这个数变成负数。具体来说,假设我们还是想表示 \((-7)_{10}\) 这个数,此时在 Two’s-Complement 编码下,他会被表示为
\[(1001)_2 = 2^0 + (-2^3) = 1 – 8 = (-7)_{10}\]
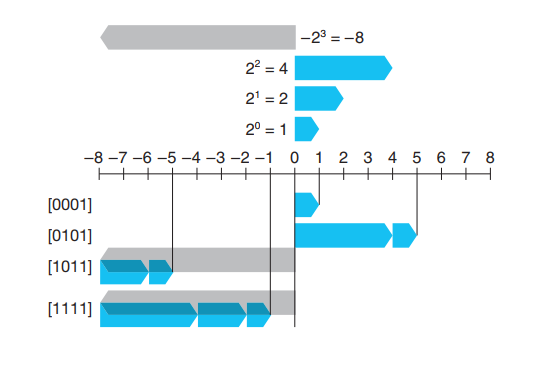
注意最高位上原本应该代表 \(2^3\) 的位现在变成代表 \(-2^3\) 了,别小看这一个小小的修改,它解决了我们之前那个设计的所有问题!
对于0来说,只有 \((0000)_2\) 能代表0, 不会出现之前的逻辑错误。在做加法的时候,直接按照二进制规则加就行了,不用做任何额外操作,比如 \( (4)_{10} + (-3)_{10}\) 就是
\[(0100)_2 + (1101)_2 = (0001)_{2} = (1)_{10}\]
注意计算的时候 \( (0100)_2 + (1101)_2 \) 虽然在最高位上加法出现了进位,但是我们直接把进位丢弃即可,因为此时我们假设只用4位来表示数字,32位同理。如果是减法,我们只要把 \(A-B\) 转化为 \(A+(-B)\) 然后进行加法运算就好了。现在有个问题,如何求出 \(-B\) 呢?也就是如何根据一个数的二进制表示求出其相反数呢?
很简单,对这个数的二进制位各位取反,末尾加一。比如我们知道在4位表示下 \((3)_{10} = (0011)_{2}\),那么-3就是 \( (1100)_2 + (0001)_2 = (1101)_2\) 这个数在 Two’s-Complement 编码下就是:
\[ (1101)_2 = 2^0 + 2^2 – 2^3 = 1 + 4 – 8 = -3 \]
各位取反和末尾加一这两个操作都可以极其方便的在电路中实现。除了加减,你会发现这个编码对于乘法和除法也有良好的支持,不过这里不再过多讨论。Two’s-Complement 编码也有缺点的,对于人类来说,这个编码不太好解读(反正计算机好解读就行了),同时它必须保证这个数字在一定的位数下才是有效的,但是正好计算机就是这么表示的。比如说 \(-1\) 这个数,二进制表示就是全1,根据存储的位数,如果是32位带符号整数,就是32个1,如果是16位就是16个1。总而言之,Two’s-Complement 编码对于计算机的存储简直就是完美的表示方法。最后一个问题,为什么负数会能够多表示一个数呢?留给读者思考。
帮我计算一下 \( (-114514)_{10} \) 的二进制表示吧?假设我们用32位来存储这个整数。
知道了整数的编码了以后,我们就可以用这些知识解释一些问题了,比如int超过最大值了会怎么样?假设我们写 int x = 2147483647 + 1;,那么x的值会是什么呢?比如我混用了unsigned int和int,那么int里的-1对应的unsigned int的值应该是多少呢?
实数编码
接下来我们来讨论一下实数应该怎么表示。首先我们要明确一点,就是一个n位的二进制串最多只能有 \(2^n\) 种变换方式,所以无论怎么编码,都只能表示 \(2^n\) 种信息。但是我们的小数,或者说实数域有多大呢?哪怕是0到1之间都有无穷个实数,所以我们用 \(2^n\) 种变化无论如何都不可能把所有实数都表示出来的。所以计算机中的实数编码只是对实数域的一个近似表示。
我们先从定点数说起,对于一个长度为32位的,二进制数据,最多只能表示 \(2^{32}= 4294967296\) 种信息,假设我想表示\(0\sim 2^{16}-1\)这个区间的小数。如果我们假设所有值之间的距离都是相等的,就像整数那样,那么这个就叫定点数。其实就相当于我们把 \(0\sim 2^{32}-1\) 这个值域压缩到了 \(0\sim 2^{16}-1\) 里面而已。那么每个相邻的二进制表示之间的距离(刻度?)就是 \(\frac{1}{2^{16}} \approx 1.52\times 10^{-5}\),我们只要把这段所表示的整数除以 \(2^{16}\) 就是它表示的实数了。有个名词叫unit in last place (ULP),就是最低位增加1会对整体表示的值增加多少,可以说成是刻度,这里的ULP显然就是 \(2^{-16}\) 。
另一种解读方法是我把小数点放在了第16位之后,原先每一位从高到低表示的是
\[ 2^{31}, 2^{30}, \dots, 2^{16}, 2^{15}, \dots, 2^1, 2^0 \]
定点数相当于把整体除以了 \( 2^{16} \) 把小数点放在了中间
\[ 2^{15}, 2^{14}, \dots, 2^{1}, 2^0, \cdot, 2^{-1}, \dots, 2^{-15}, 2^{-16} \]
定点数的好处在于计算简单,只要进行正常的整数运算即可。然而,定点数的ULP很大,这意味着它不能表示很高精度的数。同时,如果增大ULP,那么能表示的值域就会变小。
那么作为一个人类,自然是要奔着我全都要的这个思想了,有没有一种方法既能表示很大的数,又能有不错的精度呢?想得美,当然没有
鱼和熊掌没法兼得,但是我们不妨放宽一点限制,我们不需要很高的绝对精度,只要相对精度在接受范围内就行了。大部分时候,只要相对于这个数本身来说,误差在百分之多少以下就可以算是能接受了。也就是说,如果我们刻度的大小随着数值的增大而增大,我们是可以接受的。
那么接下来要介绍的IEEE 754浮点数编码就是这么一种编码方式,也是目前电脑上最主流的实数编码方式,C#中的float类型和double类型都是使用了这种编码格式。其实它跟定点数的思想很像,之前的定点数相当于小数点位置是固定的,而我们浮点数就是小数点的位置不是固定的。

IEEE 754格式的编码由三部分组成,最高的一位是符号位(sign bit),随后用了8位代表指数(exponent),最后23位代表有效数字(草,这个有叫fraction的,也有叫significand的,还有叫mantissa的)。一般情况下,IEEE 754浮点数所表示的数字为:
\[ S\times 1.M \times 2^{E-127}\]
其中S是符号位,代表这个数是正还是负,M代表的就是有效数字,E代表的是指数。注意到这里我们有了符号位,之前才说过符号位有很多问题,那么为什么这里不用 Two’s-Complement 补码编码呢?这里面有很多设计上的考量,我也不太能解释清楚,如果有兴趣可以去看看当年IEEE 754标准的文档。至于-0和+0的问题,在浮点数里,负0是有意义的,因为它可以代表浮点数发生了下溢出。当某个数比0小,但是接近到无法用浮点数表示的时候,-0就可以用来代表这个值,此外,-0与其他值的互动也是和+0不同的,具体不再多说。但是在浮点数的体系里,-0和+0真的是不同的,他们代表的不是真实的数学。
回到浮点数的表示,我们可以看到图中的IEEE浮点数每个区域的位置,对于0.15625这个实数来说,它在图中被表示为
\[1 \times (1.01)_2 \times 2^{(01111100)_2-127} \]
这里有几个地方需要注意,第一,有效数字区域代表的数字一定都是 \(1.M\),也就是说对于这23位二进制串,实际从高到低每一位的数是:
\[2^{-1}, 2^{-2}, \dots, 2^{-23} \]
最后结果加上1.0,所以图中所对应的有效数字整体为 \((1.01)_2 = (1.25)_{10}\)。为什么一定要在前面加一个1.0呢?因为如果不加的话,同一个数就有可能有很多种表示方式,只要你改变指数位的值,并且把有效位部分进行左右移动。比如\((1.01)_{2} = (0.101)_2 \times 2\),这样就会导致能表示的数字大大减少。
第二个要注意的是,指数位所表示的数据要减去127,其实这个地方就很像我们之前说的补码,只不过是直接减去一个定值。那么图中的指数位所表示的是 \((01111100)_2 = 124\),减去127就是-3。所以图中这个值的正确表示应该是:
\[1.25 \times 2^{-3} = 1.25 \times 0.125 = 0.15625\]
来练练手吧:计算一下 \(01000111110111111010100100000000\) 这串IEEE754浮点数编码所代表的实际小数是多少?(提示:一个数乘以 \(2^k\) 相当于把它的二进制表示向左移动k位)
再来试试这串吧 \(01000100111011111111100111101100\)(提示:计算二进制的时候小数,可以先把小数点全部移到后面,然再在把得到的十进制数除以\(2^k\))
1.0这个数表示成IEEE754编码应该是多少?0.0这个数呢?
在1~2这个范围内,我们的指数位 \( E-127 \) 为0,此时值为 \(1.M\),所以我们的有效位这时候就像一个小数点后面可以有23个二进制位的定点数,那么它的ULP或者刻度为 \(2^{-23} \approx 1.192\times 10^{-7}\)。如果这个数在1024~2048这个范围内,那么指数位减去127以后就会是10,所以小数点后面虽然仍然可以有23个二进制位,但是解释的时候会乘以一个 \(2^{10}\),导致刻度其实增大了 \(2^{10}\) 倍,此时ULP为 \(2^{-13} \approx 1.22\times 10^{-4}\)。可以说,绝对精准度下降了 \(2^{E-127}\) 倍。这就是我之前所说的刻度的大小随着数值的增大而增大,它保证了每个指数都有\(2^{23}\)个刻度,在此过程中,小数点的位置相当于随着 \(E\) 的变化一直漂浮不定,所以称为浮点数。
我之前说过一般情况下,IEEE754浮点数是可以用那个公式转化为实数的,但是为什么是一般情况下呢?如果你有认真想过我提的几个问题,在你表示0.0这个数的时候你就会遇到问题。事实上,用这种表示方法是没法表示0这个数的,即使你全部位都设为0,表示的其实也是
\[1.0\times 2^{-127} \approx 5.877\times 10^{-39}\]
这显然不符合逻辑,0这么重要的东西怎么能没有呢?而且位全为0如果还不表示0,是不是有点别扭?于是IEEE754浮点数标准在规定的时候单独列出了\(E-127 = -127\)这种情况下的取值。一旦指数是 \(-127\) ,那么表示的数变成:
\[S \times 0.M \times 2^{-127}\]
这种表示方式被称为非规范(Denormalized)表示,之前的那个叫做规范(Normalized)表示。\(1.M\) 变成了 \(0.M\) 而已,为什么可以这样做呢,因为-127已经是最小的指数了,如果 \(M\) 存在再小的值也没有其他的方式去表示了,所以不会出现一个数被表示多次的情况。
在非规范表示下,0就可以被表示为全0的二进制串了。
除此之外,IEEE754浮点数标准还规定了当 \(E=255\) 的时候的取值,此时指数为128。在指数位全为1的情况下,如果有效数字全为零,那么这时该浮点数表示的就是无穷大,根据符号位确定是正无穷还是负无穷,通常如果你进行1.0/0.0这样的操作,就会返回无穷大。
在指数位全为1的情况下,如果有效数字位不是全0,那么此时这个浮点数代表的就是NaN(Not a number 非数字)。0.0/0.0这个操作就可以得到一个NaN。值得注意的是,任何算数操作符碰到NaN都会返回NaN,并且NaN永远不会等于自己。所以C标准库中用 \(!(x==x)\) 来判断一个数是不是NaN。
试着计算一下,浮点数能表示的最大值和最接近0的正实数分别都是多少?最小的值是多少?
总结一下,浮点数一共有4种表示方法
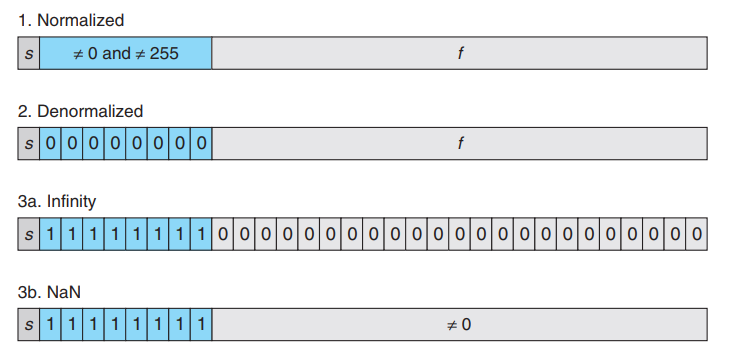
- 规范表示法:当且仅当E(没有减去127)不为0或者255。计算方式为 \[ S\times 1.M \times 2^{E-127}\]
- 非规范表示法:当且仅当E(没有减去127)为0。计算方式为 \[ S \times 0.M \times 2^{-127}\]
- 无穷大:当E(没有减去127)为255,且有效数字位全为0的时候,表示无穷大。
- NaN:当E(没有减去127)为255,且有效数字位不为0的时候,表示非数字。
图中32位表示的就是32位单精度浮点数(float)的格式,如果是64位的双精度(double)数据类型,格式也是差不多的,就是指数位变成了11位,有效数字位变成了52位,并且E要减去的值也变成了1023。
试着计算一下,双精度浮点数能表示的最大值和最接近0的正实数分别都是多少?最小的值是多少?
一般来说,如果数本身越大,它的精度越低,如果本身越接近0,那么精度越高,这个精度指的是绝对精度。所以在使用浮点数进行计算的时候,不要惊讶于为什么结果和预期有偏差。在把实数变成浮点数的时候,有时候这个数不在刻度上,我们就需要一些规则去决定这个数应该被表示为哪个相邻的刻度,这些也叫做取整规则。
最后说一下如何把十进制小数转为二进制小数,假设我们要把 \(10.1\) 这个十进制小数变成二进制小数,我们可以先分开小数点左右两边,对于左边直接用之前的模2除以2方法得到一个二进制串:\( (1010)_2 \)。对于右边则进行乘以2取整的操作,以0.1为例
\[ 0.2 \to 0\]
\[ 0.4 \to 0\]
\[ 0.8 \to 0\]
\[ 1.6 \to 1\]
\[ 1.2 \to 1\]
\[0.4 \to 0\]
\[0.8 \to 0\]
(无限循环)
所以结果为\( (1010.000110011\dots) \),如果我想把它转化为IEEE754单精度浮点数,那么可以把小数点移到首位后面。此时指数位的值为 \(3\),\(E=(3+127)_{10} = (1000 0010)_{2}\),\(M = (1.01000011001100110011001)_2\),符号位自然是0了,所以最终结果为:
\[(01000001001000011001100110011001)_2\]
试着把以下数转化为IEEE754浮点数编码,写出其二进制串,并且将编码解码后的值与原值做对比:\(0.142857,10^{30},\sqrt{2},\pi\)