适配版本 (1.4.4ver)
本章我们将会继续学习,弹幕有关的数学知识。
三角函数
上一讲中,我们提到,向量是具有大小和方向的量,并且学会了向量之间的运算。但是这些运算都是基于向量X,Y分量的,如果我们只知道向量的长度和与X轴正方向的夹角,那我们怎么求出向量的 \((x, y)\) 两个分量呢?
当然可以,我说过 \((x,y)\) 表示法已经包含了向量的所有信息(大小方向),那么知道大小和方向也就能知道 \((x,y)\) 了,这个关系是一一对应的。
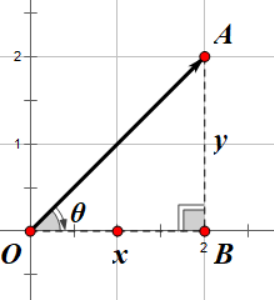
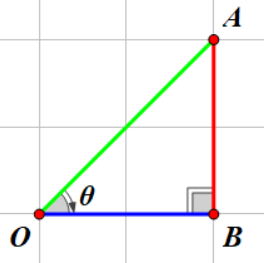
如图,我们想求向量 \(\overrightarrow{OA}\) 的 \(x, y\) 分量大小,我们知道向量的长度 \(|\overrightarrow{OA}| = l\) ,以及向量与x轴正半轴的夹角 \(\theta\) , 如果你没有学过三角函数,那么可能会不知所措,但是我可以告诉你答案是 \(x = l\cos(\theta), y = l\sin(\theta) \) 。
诶,等等这个 \(\cos, \sin\) 是什么东西?不会是什么高深的数学知识吧,我不学了!(如果有学过了的请无视)
等等,虽然看起来比较难,但是你没得选择,因为在TR里面,很多情况下都需要用三角函数来操作向量的角度,比如散射,追踪,周期运动。如果你不知道三角函数你可能就没办法写出这么有意思的AI了QAQ。
定义
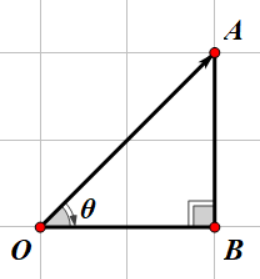
三角函数三角函数,肯定得有一个三角形,但是这个三角形不是普通的三角形,而是一个直角三角形。正如上图中的三角形\(OAB\),我们重新画一下这个三角形。
因为我们目前只关注 \(\theta\) 这个角,所以就以这个角为基准,我给你们介绍几个定义:
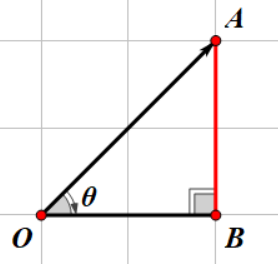
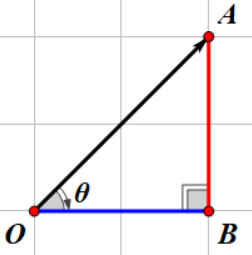
对边(Opposite):与这个角正对着的边,也就是 \(\overline{AB}\) ,在图中标记红色。
邻边(Adjacent):与这个角相邻的直角边,也就是 \(\overline{OB}\) ,在图中标记蓝色。
斜边(Hypotenuse):最长的那条斜边,也就是 \(\overline{OA}\),也就是我们要求的向量所代表的线段,在图中标记绿色。
这几条边搞清楚的弹幕扣波6,然后我们就可以定义什么是三角函数了!
\(\sin(\theta)\):对边与斜边长度的比值,写成分数是这样的\[\frac{\text{对边}}{\text{斜边}} = \frac{|\overline{AB}|}{|\overline{OA}|}\] 或者红色边除以绿色边。
注意,不管他们的具体长度是多少,我们只要知道 \(\theta\) ,我们就知道了他们长度的比值,而我们只关心这个比值。还有,方向不要搞反哦,是对边比斜边。
\(\cos(\theta)\):邻边与斜边长度的比值,写成分数是这样的\[\frac{\text{邻边}}{\text{斜边}} = \frac{|\overline{OB}|}{|\overline{OA}|}\] 或者蓝色边除以绿色边。
除了这两个函数还有一个特别重要的 \(\tan(\theta)\)。
\(\tan(\theta)\):对边与邻边长度的比值,写成分数是这样的\[\frac{\text{对边}}{\text{邻边}} = \frac{|\overline{OB}|}{|\overline{OA}|}\] 或者红色边除以蓝色边。
所以为啥我们的结果是 \(x = l\cos(\theta), y = l\sin(\theta) \) 呢?此时我们斜边(向量)的长度是 \(l\),那么我们可以这么写
\[\text{对边长度} = \text{斜边} \cdot \frac{\text{对边}}{\text{斜边}} = \text{斜边} \cdot \sin{\theta} = l\sin{\theta}\]
对不对?如果我们回头看一下那张图,对边正好就是我们要求的 \(y\)。同理,我们想要得到邻边长度可以这么写:
\[\text{邻边长度} = \text{斜边} \cdot \frac{\text{邻边}}{\text{斜边}} = \text{斜边} \cdot \cos{\theta} = l\cos{\theta}\]
而我们的邻边正好就是向量的 \(x\) 分量。所以知道了角度和长度我们就可以知道向量的坐标了。我们就可以这么生成一个固定长度和方向的向量:
float r = 角度, d = 长度; Vector2 vector = new Vector2(d * (float)Math.Cos(r), (float)Math.Sin(r));
知道了,这就去和散射对线……生成不同角度的弹幕!
等等,如果你直接把角度写进\sin和\cos函数里,你可能得不到正确的向量,为什么呢?因为XNA(以及C#标准库)系统使用的是弧度(Radius)制而不是我们所熟悉的角度(Degree)制(虽然说我个人更喜欢弧度制,但是并非每个人都是这样),比如说30度角,在弧度制里面就是\(\frac{\pi}{6}\)。
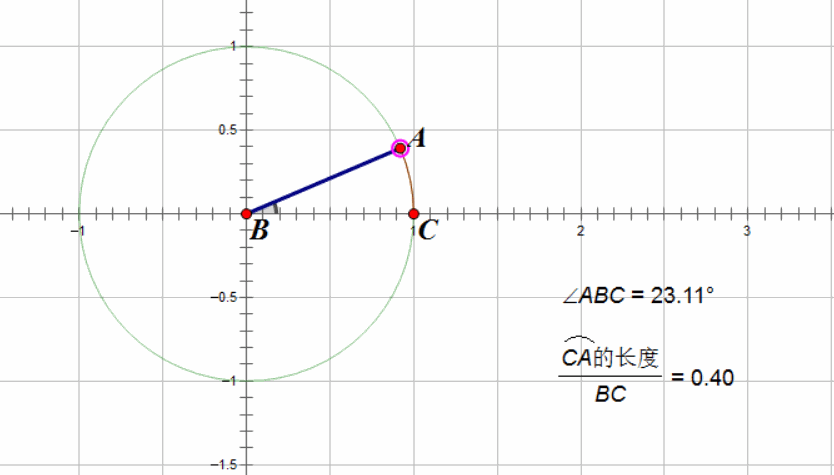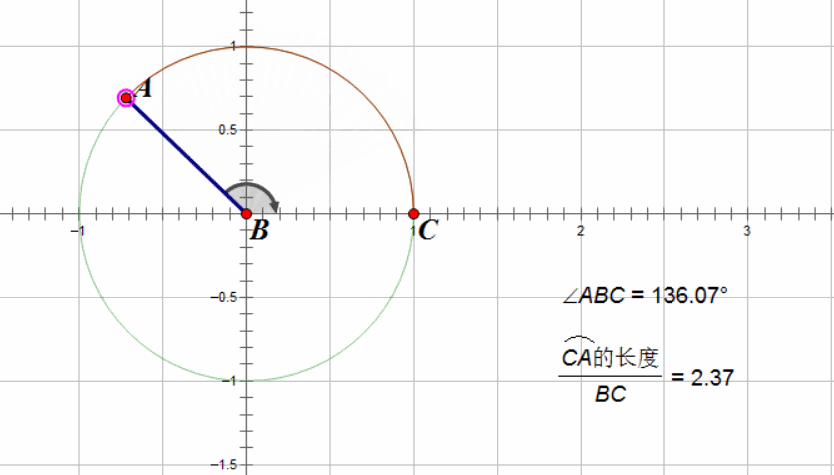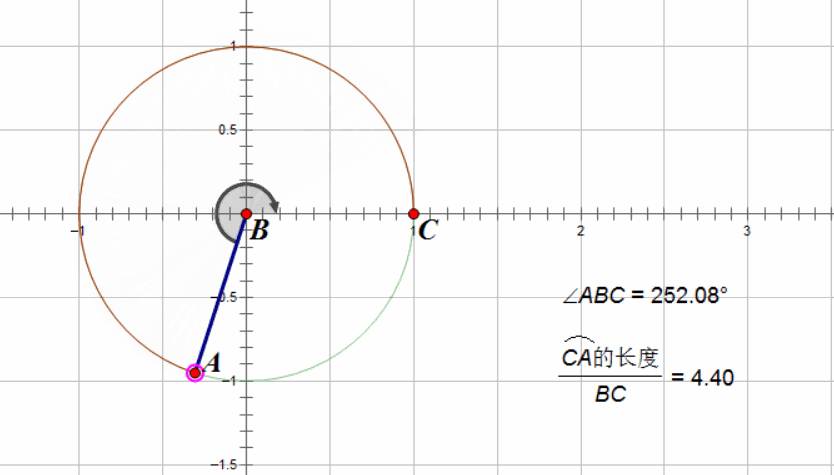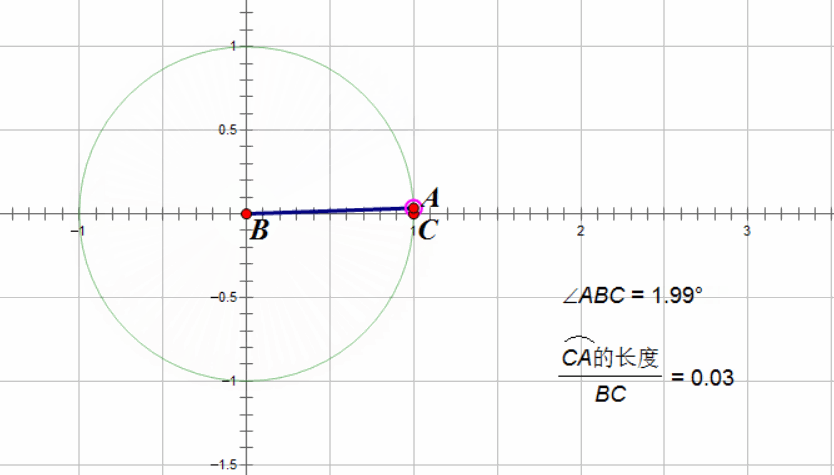
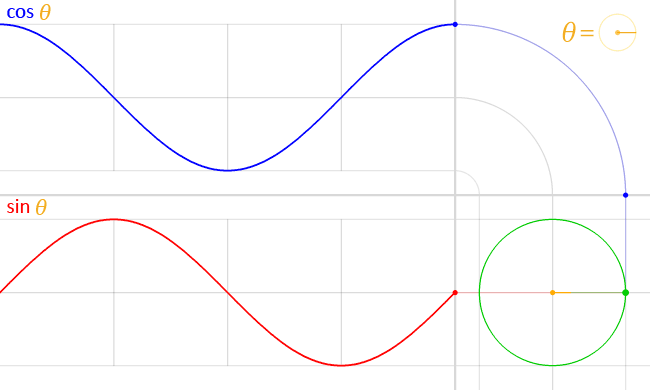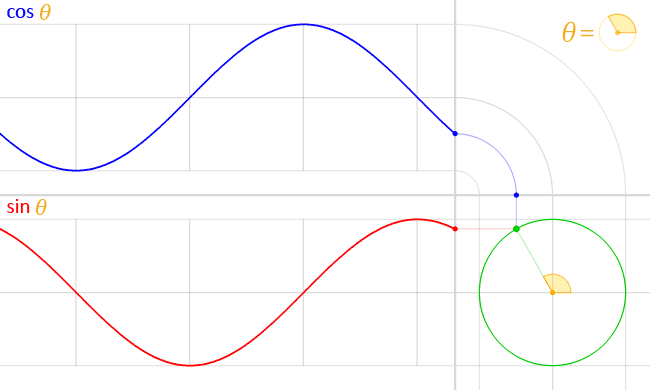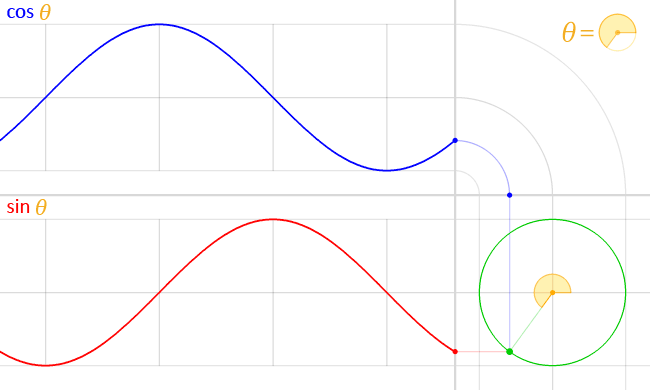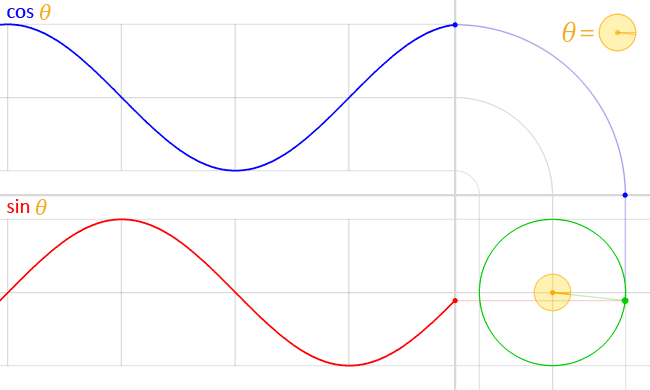
所以什么是弧度呢?其实就是在圆的半径为1的时候,在这个角度的情况下,所构成的圆弧的长度。可能不太好理解,那就用动画来解释:
此时,原来的360度角就变成了 \(2\pi\),原来的180度角就变成了 \(\pi\),总而言之,就是把原来的360度角压缩到了\([0, 2\pi)\)这个区间。
下面是一张常用三角函数表,以及其弧度
| 角度 | 0° | 15° | 30° | 45° | 60° | 90° | 120° | 135° | 150° | 180° |
|---|---|---|---|---|---|---|---|---|---|---|
| 弧度 | \(0\) | \(\frac{\pi}{12}\) | \(\frac{\pi}{6}\) | \(\frac{\pi}{4}\) | \(\frac{\pi}{3}\) | \(\frac{\pi}{2}\) | \(\frac{2\pi}{3}\) | \(\frac{3\pi}{4}\) | \(\frac{5\pi}{6}\) | \(\pi\) |
| \(\sin\)值 | \(0\) | \(\frac{\sqrt{6} – \sqrt{2}}{4}\) | \(\frac{1}{2}\) | \(\frac{\sqrt{2}}{2}\) | \(\frac{\sqrt{3}}{2}\) | \(1\) | \(\frac{\sqrt{3}}{2}\) | \(\frac{\sqrt{2}}{2}\) | \(\frac{1}{2}\) | \(0\) |
| \(\cos\)值 | \(1\) | \(\frac{\sqrt{6} + \sqrt{2}}{4}\) | \(\frac{\sqrt{3}}{2}\) | \(\frac{\sqrt{2}}{2}\) | \(\frac{1}{2}\) | \(0\) | \(-\frac{1}{2}\) | \(-\frac{\sqrt{2}}{2}\) | \(-\frac{\sqrt{3}}{2}\) | \(-1\) |
| \(\tan\)值 | \(0\) | \(2-\sqrt{3}\) | \(\frac{\sqrt{3}}{3}\) | \(1\) | \(\sqrt{3}\) | ? | \(-\sqrt{3}\) | \(-1\) | \(-\frac{\sqrt{3}}{3}\) | \(0\) |
应用
然后你就可以去对线了,我们先试着做一个朝8个方向发射的弹幕吧?同样还是找到Shoot函数,写下这些代码:
// 把圆分成8等分,然后每个角度都发射一个向量
for (float r = 0f; r < MathHelper.TwoPi; r += MathHelper.TwoPi / 8f) {
// 发射速度是与x轴正半轴夹角为r,长度为
Vector2 velocity = new Vector2((float)Math.Cos(r), (float)Math.Sin(r)) * 10f;
Projectile.NewProjectile(source, position, velocity, type, 100, 10f, player.whoAmI);
}
此外你还可以给每个发射角一个固定的旋转角度,甚至两个分量的角度不同,然后把发射的数量增加,比如这样:
// 把圆分成8等分,然后每个角度都发射一个向量
for (float r = 0f; r < MathHelper.TwoPi; r += MathHelper.TwoPi / 8f) {
// 发射速度变得诡异了
Vector2 velocity = new Vector2((float)Math.Cos(r + 0.5f), (float)Math.Sin(r - 0.5f)) * 10f;
Projectile.NewProjectile(source, position, velocity, type, 100, 10f, player.whoAmI);
}
原版有提供生成单位向量的方法,但是我仍然推荐直接使用 \(\cos{\theta}, \sin{\theta}\),因为它能自定义一些奇奇怪怪的行为
// 更方便的向量生成 Vector2 velocity = r.ToRotationVector2() * 10f;
但是这个弹幕发射的角度固定啊,怎么样才能获取发射到鼠标位置的角度呢?
我之前说过,角度、长度和向量的坐标形式是一一对应的,那么通过向量的坐标形式一定也能获取长度和角度,长度我们上一章讲过了,那么角度呢(你不用长度就能知道角度)?这时候就要用我们的反三角函数了。
反三角函数
什么是反三角函数呢?我们知道角度为 \(\theta\) 的向量的\(x,y\)的比值是 \(\cos{\theta}, \sin{\theta}\) 那么如果给你某个向量的 \(x,y\) 比值我们是不是可以反过来求出 \(\theta\) 呢?当然可以,比如给你向量 \((0,1)\) 你一定知道它与x轴正半轴的夹角是90度。同理,假设给你一个对边比斜边的比值,你是否可以求出角度呢?
那么这种函数就叫做反三角函数:给你某两条边的比值,你返回一个弧度。比如 \(\sin\) 的反函数可以记做 \(\sin^{-1} (x)\),或者 \(\arcsin (x)\),注意,这里的 \(-1\) 可不是-1次方哦,而是反函数的标记。如果是-1次方会是这样 \((\sin(\theta))^{-1}\)。
以下内容可以略读 略读开始标记————————————————————>
但是数学上的反函数有一个缺点,比如说我们看看下面这张三角函数图
圈还没有转完但是 \(\sin\) 和 \(\cos\) 函数却有两个波峰/波谷,也就是说同样的一个值会出现两次,那么我们怎么知道反过来的这个角度是哪一个呢?
我们确实没法知道,所以我们规定反三角函数返回的角度 \(\sin^{-1}\) 在 \([-\frac{\pi}{2}, \frac{\pi}{2}]\)(我们可以把 \(\sin\) 值想象为向量的y坐标,仔细看看上图,你发现了什么?)
\(\cos^{-1}\) 在 \([0, \pi]\)(我们可以把 \(\cos\) 值想象为向量的x坐标,仔细看看上图,你发现了什么?)
也就是说,我们并没法确定这个反sin函数是30度还是150度,但是我会返回给你30度( \(\frac{\pi}{6}\) )。
但是我们却是可以准确得到向量的角度,为什么呢?因为我们还可以判断这个向量x,y分量的正负啊!如果这个向量在第一象限,那么 \(x, y\) 都是正的(也就是说 \(\cos\) , \(\sin\) 都是正的),第二象限 \(x\) 是负的, \(y\) 是正的(也就是说 \(\cos\) 是负的, \(\sin\) 是正的),以此类推,我们就能够知道处在第几象限了,然后我们只要把xy都变成第一象限,求一下与x轴的夹角,然后再转回之前求的象限就是真实的角度了!
但是用 \(\cos^{-1}\) , \(\sin^{-1}\) 求这个有点麻烦,别忘了我们还有 \(\tan^{-1}\) 这个反函数。那么我们可以得出向量转角度的算法:
- 先根据正负确定 \(\vec{v} = (x, y)\) 在第几象限
- 令 \(\vec{u} = (|x|, |y|)\)
- 求出 \(r = \tan^{-1} (\frac{|x|}{|y|})\)
- 然后把 \(r\) 加到每个象限对应的实际角度,比如第一象限是 \(0+r\),第二象限 \(\pi-r\),第三象限 \(\pi+r\),第四象限 \(0-r\)(大家可以画个图然后推一下)
略读结束标记 ————————————————————>
C#提供了求这个角度的方法,我们的Math.Atan2这个函数就是干这个的,它和Math.Atan的区别就在于之前所说的,Atan只能返回不重复的弧度(角度)值,而Atan2能返回正确的弧度。使用方法为:
// 注意,这个函数的第一个参数是y,因为我们要先传入对边嘛,tan是对边除以邻边 float r = (float)Math.Atan2(velocity.Y, velocity.X);
有了它,我们就可以获取向量角度然后做一些事情了!比如散射,我们要做的是:
- 获取从玩家到鼠标的向量
- 计算向量的弧度 \(r\)
- 通过这个弧度生成一些偏移角度,比如左右10度的向量
- 把这些弧度全部计算成发射的向量,然后把弹幕发射出去
于是我们可以在Shoot里写代码:
// 计算玩家中心到鼠标的向量,Main.MouseWorld就是鼠标在世界的位置
Vector2 plrToMouse = Main.MouseWorld - player.Center;
// 计算玩家到鼠标的向量弧度
float r = (float)Math.Atan2(plrToMouse.Y, plrToMouse.X);
// 五个散射弹幕 分别偏移 -10 -5 0 5 10 度
// 5度 = pi/36 弧度
for (int i = -2; i <= 2; i++) {
// 发射向量的弧度,给原来的弧度加了一些偏移:-2*5 = -10, -1*5 = -5 ...
float r2 = r + i * MathHelper.Pi / 36f;
Vector2 shootVel = r2.ToRotationVector2() * 10;
Projectile.NewProjectile(source, position, shootVel, type, 100, 10, player.whoAmI);
}
于是我们就能发射散弹了!
那么到此为止,你已经掌握了tr物体运动的基本规律了,也可以去操作这些向量使得他们按照你的意愿运动了,还有就是要善用三角函数哦,它的周期性非常美,弹幕用上它轨迹也会变得非常优美,比如:
// 让弹幕按照sin函数的周期性旋转,旋转弧度范围为[-0.5, 0.5] float r = (float)Math.Sin(Main.time) * 0.5f; // 哈哈,这是个内置的写法,能减少你的代码量(不用写Atan2和Cos,Sin了) Projectile.velocity = Projectile.velocity.RotatedBy(r);
当然,这只是数学之美的冰山一角,多去探索,你会爱上数学的。