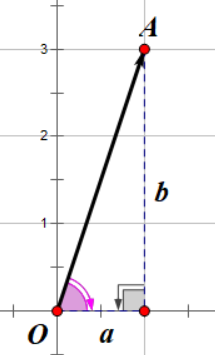跳至正文

向量基础

适配版本 (1.4.4ver)

向量（Vector）

为了真正发挥弹幕（以及Mod其他内容）的作用，我们一定要对向量，位置，等概念有充分的了解，这也是Mod制作的重点。在Mod制作中，我们只关注平面向量（因为TR是个2D游戏啊）。

定义

平面向量是在二维平面内既有方向(direction)又有大小(magnitude)的量。与之相对的是只有大小、没有方向的量（标量，如\(0.142857, 200000\)）。

TR所有的物体的运动情况都是用向量表示的，比如说：

这些白色箭头都是物体的速度向量，箭头越长代表这个物体的速度越大。你会发现，除了有长短以外，还有方向，这就是向量的定义了。

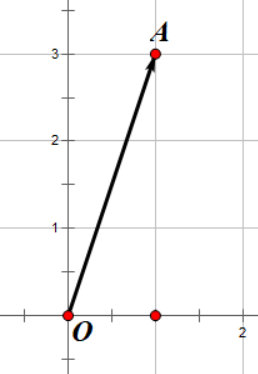
假设玩家往上跳的时候有一个速度向量，我们在坐标轴中画出这个向量，应该差不多长这个样子：

图中的从\(O\)点开始，指向\(A\)点的向量就是玩家的一个速度向量，我们把它记作向量 \(\overrightarrow{OA}\) ，或者也可以记作\(\boldsymbol{OA}\)（变粗了而已。如果向量是从 \(A\) 到 \(O\)，那我们就要记做 \(\overrightarrow{AO}\)，这里的方向很重要，因为向量是包含方向的嘛。

图中的这个向量起点是 \(O(0, 0)\) ，终点是 \(A(1, 3)\) ，所以我们还可以把这个向量表示为二元组形式（或者说是坐标形式，反正就那个意思）：\(\overrightarrow{OA} = (1, 3)\)。或者说，这才是向量的本体。

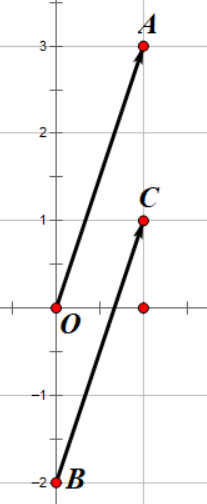
假设我们有另一个向量 \(\overrightarrow{BC}\) ，从起点 \(B(0, -2)\) 到终点 \(C(1, 1)\) ，那么它的坐标表示形式为

\[\overrightarrow{BC} = C-B = (1,1)-(0, -2) = (1, 3)\]

我们就可以说 \(\overrightarrow{OA} = \overrightarrow{BC}\) ，因为他们的坐标形式相同。

也就是说我们并不关心这个向量是从哪个点到哪个点，我们只关心它的大小和方向。

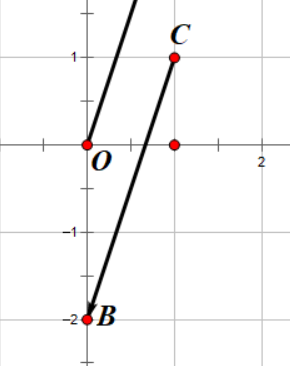
如果我们考虑的向量是 \(\overrightarrow{CB}\) ，那么它的坐标形式为

\[\overrightarrow{CB} = B-C = (0,-2)\ -\ (1, 1) = (-1, -3)\]

可以看到，它的坐标形式刚好就是 \(\overrightarrow{BC}\) 的相反数。诶，那么我们是不是可以说 \(\overrightarrow{BC} =\ – \overrightarrow{CB} \) 了呢？确实如此，事实上我们这可以看做是对向量的运算。

向量运算

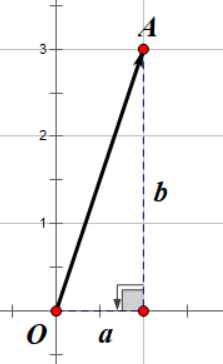
首先，向量有长度，那么它的长度是什么呢？你们应该都知道勾股定理吧，怎么求一个直角三角形斜边长度。向量也是一样。

假设有一个向量 \(\vec{v}\) ，同时 \(\vec{v} = (a, b)\) 那么我们记向量 \(\vec{v}\) 的长度 \(|\vec{v}|\) ，为\[ |\vec{v}| = \sqrt{a^2 + b^2}\]

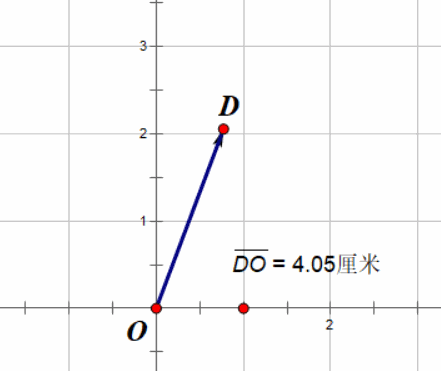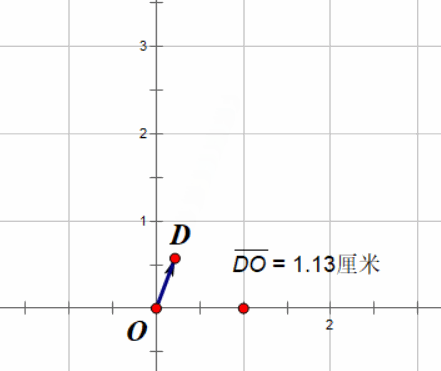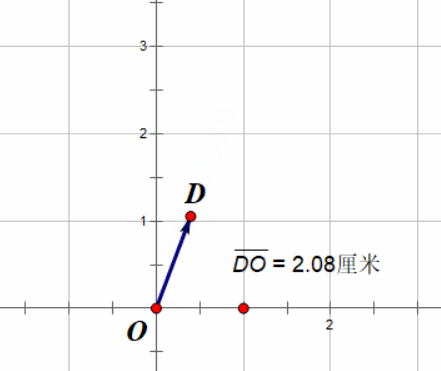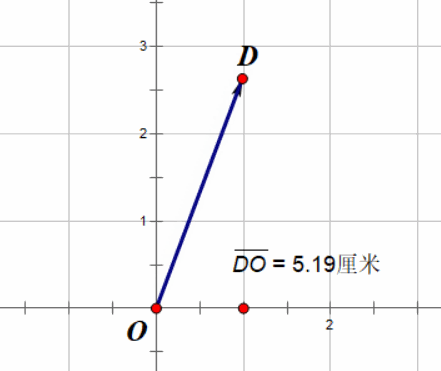
如果我们把这个向量的坐标扩大两倍会怎么样？假设我们有向量 \(\vec{v} = (1, 3)\) ，扩大两倍就变成 \(2\vec{v} = (2, 6)\) ，那么向量长度变了多少呢？

\[|\vec{v}| = \sqrt{1^2+3^2} = \sqrt{10} \\ |2\vec{v}| = \sqrt{2^2+6^2} = \sqrt{40} = 2\sqrt{10}\]

所以，向量长度扩大了两倍。那我们是不是可以推出来，假设有一个常数 \(c\) ，那么

\[ |c\vec{v}| = c |\vec{v}| \] 证明

设向量 \(\vec{v} = (x, y)\)，那么 \(c\vec{v} = (cx, cy)\)
那么长度为 \(|c\vec{v}| = \sqrt{c^2x^2+c^2y^2} = \sqrt{c^2(x^2+y^2)} = c\sqrt{x^2+y^2} = c|\vec{v}|\)

其次向量有方向，向量的方向其实就是与x轴正半轴的夹角，它的计算方式我们之后在说。

现在想象一下另外一个场景，玩家在奔跑的时候起跳，此时跳跃只有一个向上的向量，但是玩家的速度向量是水平的，那么跳跃的时候速度向量应该是什么样的呢？

，起跳的向量变化

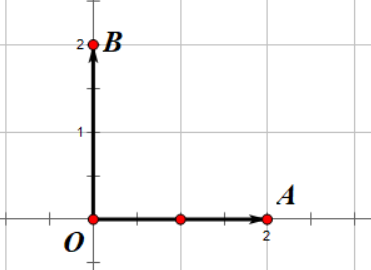
我们可以把玩家速度和跳跃速度画在平面直角坐标系中：

然后我们定义向量的加法操作为，假设有向量 \(\vec{v} = (a, b)\) ，\(\vec{u} = (c, d)\) ，那么 \(\vec{v} + \vec{u} = (a + c, b + d)\)

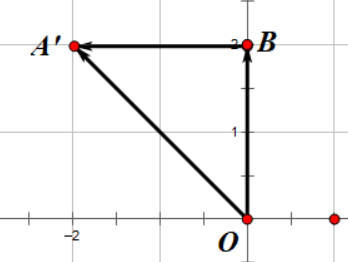
很简单不是吗？但是这个操作为什么有意义呢？假设以上图为例，我们把向量 \(\overrightarrow{OA}\) 接到向量 \(\overrightarrow{OB}\) 上，就像接头霸王一样，

又要迫害我了吗？

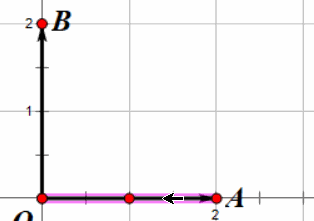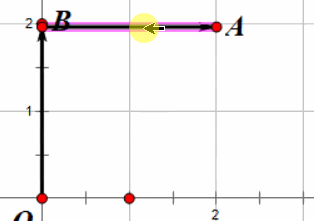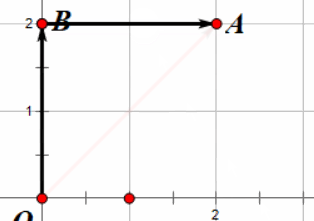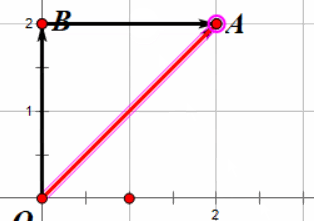
那么新的 \(\overrightarrow{OA}\) 就是我们要求的 \( \overrightarrow{OA} + \overrightarrow{OB} \)。

我们可以从图中看出，这个向量确实是 \( \overrightarrow{OA’} = (2, 2)\)，你也可以很轻易的验证其他形状的向量也是如此。所以说，向量加法本质上就是把一个向量的尾部接在另一个向量的头部。所以玩家跳跃的时候就是将玩家速度加上了一个向上的向量，我们可以在武器里面给玩家速度加上一个向量，看看会发生什么。

注意，在泰拉瑞亚世界中，坐标的原点是处在左上角，并且只有第四象限，此外，坐标的Y坐标从上到下从零开始递增。所以向上一个单位的向量其实是 \((0, -1)\) ，但是左右方向是与笛卡尔坐标系相同。

平面直角坐标系
TR坐标系

试试这个Shoot重写函数函数，位于物品文件内，其中Vector2就是我们的平面向量（来自Microsof.XNA.Framework，也就是XNA提供的），它的构造函数里面可以写x分量和y分量的值，player.velocity就是我们玩家的速度，TR世界里面玩家的位置每帧都会根据player.velocity改变，具体来说就是player.position += player.velocity，速度的大小越大，玩家位置变的也就越快。当然不只是玩家，像弹幕，NPC都会每帧更新速度。

public override bool Shoot(Player player, EntitySource_ItemUse_WithAmmo source, Vector2 position, Vector2 velocity, int type, int damage, float knockback) {
    // 武器射出弹幕的时候会给玩家一个5倍大小的速度
    player.velocity += velocity * 5f;
    return true;
}

有了加法自然会想到减法，向量的减法其实就是加法，只不过加的是反向的向量，因为反向向量就是正向的相反数。

向量的减法操作：假设有向量 \(\vec{v} = (a, b)\) ，\(\vec{u} = (c, d)\) ，那么 \(\vec{v}-\vec{u} = \vec{v}+(-\vec{u}) = (a-c, b-d)\)

它的几何意义也就很简单了：把后面的向量反向，然后把尾部接在之前的向量的头部。

OA’即为结果

本章最后再说一下单位向量，这个东西在以后制作各种弹幕和游戏内容都会非常有用。什么是单位向量，就是长度为1的向量。

当你得到一个单位向量的时候，你就可以暂时不考虑向量大小的影响而是只用考虑方向，比如说，我们求一下射向敌人的子弹的速度。假设敌人在 \(A\) 点，我们在 \(B\) 点，那么射向敌人的向量将会是 \(A-B\) 或者 \(\overrightarrow{BA}\)（注意方向）。

此时如果我们把弹幕速度直接设为 \(\overrightarrow{BA}\) ，那显然弹幕速度取决于你和敌人直接的距离，这样是不好的（要么子弹慢如蜗牛，那么快到鬼畜）。很多时候我们弹幕射出的速度大小都是固定的，那么这个时候我们最好的解决办法就是把这个向量先缩到单位向量，这样我们直接乘以我们想要的速度大小，就能得到一个速度固定，方向是射向敌人的向量了。

把向量变成单位向量的操作叫做标准化（Normalization），具体操作方法就是\[\vec{v’} = \frac{\vec{v}}{|\vec{v}|}\]

也就是把向量的长度缩放到原来的 \( \frac{1}{|\vec{v}|} \) （除以向量\(\vec{v}\)的原长度），很简单吧？注意！零向量（\(\vec{0} = (0,0)\)）没有单位向量（废话），如果你在计算的时候除以了零……

接下来我们就把刚刚说的自瞄（我没开挂）应用到游戏中吧，首先先准备一个能射出弹幕的武器。然后在Shoot重写函数里面写：

// 对于所有世界里的npc
foreach (var npc in Main.npc) {
    // 如果它活着并且是敌对生物
    if (npc.active && !npc.friendly) {
        // 射出自瞄弹幕（X）
    }
}

此时npc里面存储的就是符合条件的敌对npc了，然后我们明确一下要做的事情：

  1. 获取npc的位置，然后计算从玩家到npc的向量
  2. 把向量标准化（Normalize）
  3. 标准化以后的向量要乘以我们想要的速度
  4. 把这个速度的弹幕发射出去

于是我们可以在Shoot里写

// 对于所有世界里的npc
foreach (var npc in Main.npc) {
    // 如果它活着并且是敌对生物
    if (npc.active && !npc.friendly) {
        // 射出自瞄弹幕
        // 任务1，注意是谁减谁
        Vector2 plrToNPC = npc.Center - player.Center;
        // 任务2
        if (plrToNPC.Length() == 0) continue;
        // Length是Vector2这个结构体自带的函数，可以返回向量长度
        // 当然你也可以用Math.Sqrt(plrToNPC.X * plrToNPC.X + plrToNPC.Y * plrToNPC.Y)
        plrToNPC /= plrToNPC.Length();
        // 任务3，我们想要速度为10
        plrToNPC *= 10f;
        // 任务4，发射弹幕，关于这个函数的属性可以自己探索，下一章有介绍
        Projectile.NewProjectile(source, position, plrToNPC, type, 100, 10, player.whoAmI);
    }
}

发表回复