问题简述
这篇文章会讨论一下利用递归实现树状结构的方式,以下两种树状弹幕全部都是利用递归树生成的,然而,仅仅几个参数值的不同可以让生成出来的树显现出截然不同的风格
树形结构设计
树其实是一种特殊的图结构,只不过它一般是无向无环联通图,而且我们计算机中表示的树其实更像是倒过来的树。
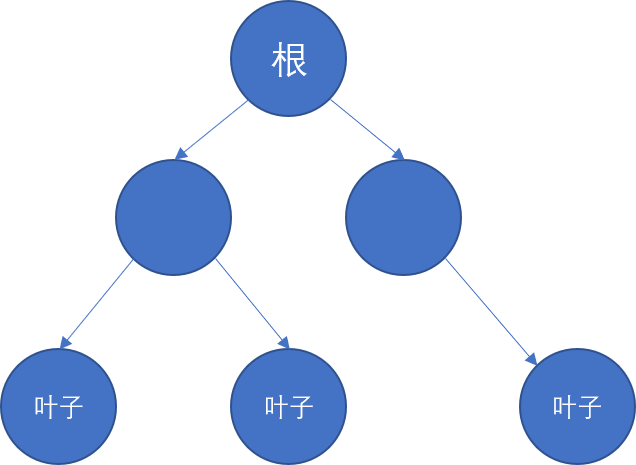
虽然说树是个无向图,但是因为每一颗树都可以定义一个根节点,所以在进行树的遍历的时候还是要从根节点向叶节点方向行进。具体来说,对于每一个非叶子节点,我们都有一些子节点悬挂在它下面:
在实现之前,我们先要了解一下为什么树形结构能够被用递归实现
- 每个子节点都可以看作其父节点的子问题,它可以在父节点的基础上更新信息
- 叶子节点可以作为递归的终止条件
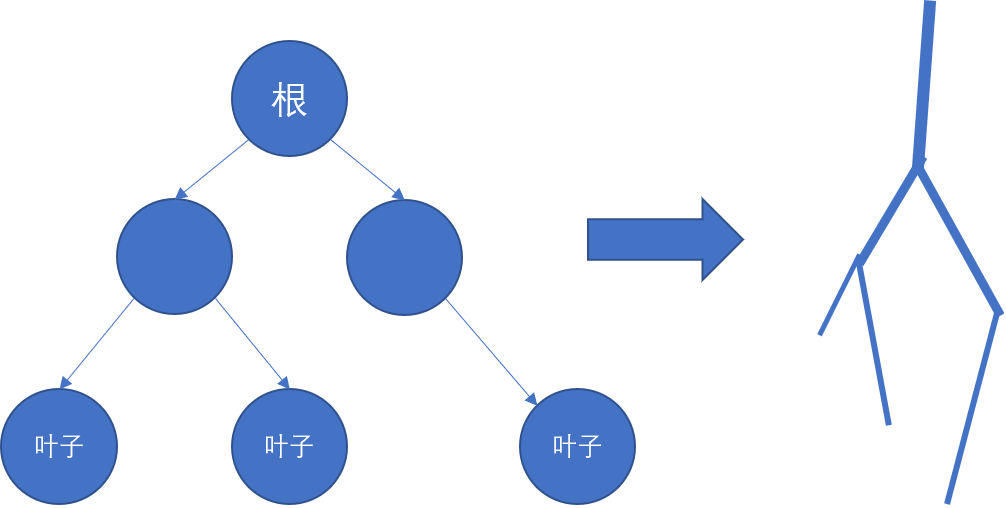
那么对于发射树状弹幕的这个问题我们要明确一点就是每个树上节点储存的信息是什么。我们首先把树状弹幕分解为一条一条的树枝,让每个节点对应一个树枝,如图
具体来说,我们的创建流程应该类似这样
啊哈,那么我们应该在每个节点上储存的信息应该就是树枝的信息了,树枝本质上就是绘制了一条线段,那么线段的信息无非就是:起点,终点。
但是为了让递归的计算量减小,我们可以加入一个辅助的朝向弧度信息,和长度信息,来替代终点这个属性,而起点变成了相对于根节点的起点,所以每个节点也不需要记录起点信息。为什么要这样做呢?因为如果我们要移动这个树,用之前的表示方法岂不是所有节点都得重新计算一遍?但是用现在的方法只需要改变根节点的位置信息,是不是可扩展性就提升很多?
说做就做,我们这样储存每个节点的信息:
public class LightTree {
private class Node {
// 每一个节点的长度,朝向,粗细(
public float rad, size, length;
// 每个节点可能有子节点,所以我们用List储存
public List<Node> children;
public Node(float rad, float size, float length) {
this.rad = rad;
this.size = size;
this.length = length;
this.children = new List<Node>();
}
};
}
整个LightTree类其实代表的就是一颗树,而Node代表了每个树上的节点,但是我们还需要一个根节点以及LightTree的构造函数,此外,为了实现随机生成的树,我们还需要一个随机数生成器。
为什么我们不用Main.rand呢?因为我们想让这棵树的形状可以随着传入的Random对象而改变,甚至支持随机种子。比如说,我们用114514这个种子生成了一颗很好看(?)的树,那么下次我们可以用这个种子再复原这棵树,所以整个类的大体框架应该是这样:
public class LightTree {
private class Node {
public float rad, size, length;
public List<Node> children;
public Node(float rad, float size, float length) {
this.rad = rad;
this.size = size;
this.length = length;
this.children = new List<Node>();
}
};
private Node root;
private UnifiedRandom random;
public LightTree(UnifiedRandom random) {
cnt = 0;
// 一开始树的根节点为空,我们需要后续的构造去给它赋值
root = null;
this.random = random;
}
}
递归构造
随机函数
生成树的随机函数我们可以使用正态分布的随机函数,这样的好处是生成出来的树的形状会比较平均,当然TR自带的Main.rand也是很好的。如果想获取正态分布的更多信息可以去这里:随机数生成入门。
private float rand() {
double u = -2 * Math.Log(random.NextDouble());
double v = 2 * Math.PI * random.NextDouble();
return (float)Math.Max(0, Math.Sqrt(u) * Math.Cos(v) * 0.3 + 0.5);
}
这个函数会生成值域在 \(-\infty, \infty\) 的浮点数,但是绝大部分(99%)的情况下值都不会超过 \(0, 1\),很大部分情况下不会超过 \(0.2, 0.8\),所以是一个比较靠谱的随机浮点数。还有就是均匀生成 \(-x, x\) 范围内浮点数的函数:
private float rand(float range) {
return random.NextFloatDirection() * range;
}
建树
首先我们要把根节点初始化,然后让递归函数递归的给根节点加上子节点,然后再给子节点加上子节点(对,就是套娃)。
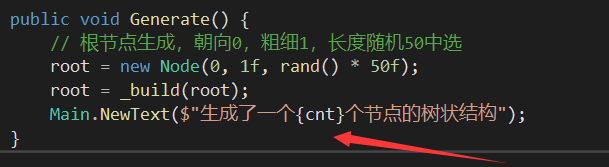
public void Generate() {
// 根节点生成,朝向0,粗细1,长度随机50中选
root = new Node(0, 1f, rand() * 50f);
root = _build(root);
}
Generate并非递归函数,而是初始化,_build才是递归函数:
private Node _build(Node node) {
// 终止条件:树枝太细了,或者太短了
if (node.size < 0.1f || node.length < 1) return node;
// 子节点数量,在2左右正态分布
int numChild = (int)(rand() * 4);
for (int i = 0; i < numChild; i++) {
// 朝向(弧度)随机旋转
// 子节点粗细程度肯定比父节点小一点嘛
// 长度也是要短一点,当然也可以变长,自己调整就好了
Node child = new Node(rand(MathHelper.Pi / 6f), node.size * 0.8f, node.length * 0.8f);
node.children.Add(_build(child));
}
return node;
}
build的主要作用就是根据父节点信息,随机生成具有随机属性的子节点,然后递归的挂在父节点上。
build结束以后我们就得到了一颗固定形状的生成树了,接下来我们要把这个树画出来,这就要使用绘制激光的技巧了。因为绘制的位置取决于玩家,或者使用这个树的程序员,而这棵树的信息都是相对根节点的,所以我们在draw的时候需要传入位置和速度信息给根节点,然后计算出实际位置才好绘制出正确的位置。
public void Draw(SpriteBatch sb, Vector2 pos, Vector2 vel) {
_draw(sb, pos, vel, root);
}
private void _draw(SpriteBatch sb, Vector2 pos, Vector2 vel, Node node) {
// 树枝实际的方向向量
Vector2 unit = (vel.ToRotation() + node.rad).ToRotationVector2();
// 类似激光的线性绘制方法,绘制出树枝
for (float i = 0; i <= node.length; i += 0.04f) {
sb.Draw(Main.magicPixel, pos + unit * i, new Rectangle(0, 0, 1, 1), Color.White * 0.5f, 0,
new Vector2(0.5f, 0.5f), Math.Max(node.size * 7, 0.2f), SpriteEffects.None, 0f);
}
// 递归到子节点进行绘制
foreach (var child in node.children) {
// 传递给子节点真实的位置和方向向量
_draw(sb, pos + unit * node.length, unit, child);
}
}
接下来我们让弹幕绘制这个树状结构,我们首先需要让弹幕在第一帧生成一棵树,之后就可以用这个树一直绘制了。首先在AI重写函数里写:
private LightTree tree;
public override void AI() {
if (projectile.ai[0] == 0) {
tree = new LightTree(Main.rand);
tree.Generate();
projectile.ai[0] = 1;
}
}
之后在Draw有关的重写函数里写:
public override void PostDraw(SpriteBatch spriteBatch, Color lightColor) {
tree.Draw(spriteBatch, projectile.Center - Main.screenPosition, projectile.velocity);
}
从图中我们就可以看出来,这个函数生成的树的节点数怕是不会少,虽然不感觉卡,但是我们不妨来统计一下它生产了多少个树节点吧?
先在LightTree里声明一个类内变量
private int cnt;
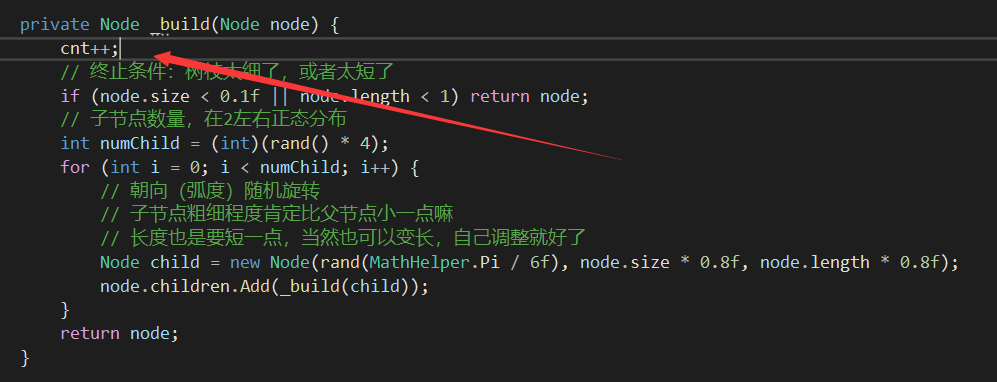
然后在建树的时候写下:
建树完成以后我们把数量显示出来:
然后你会看到:
好像也不多,如果你把build函数里面的0.8变成0.9:
这就没法承受了啊,两万多个节点的绘制,哪个受得了哦。这就是指数增长的威力了吧。
假设每个树干生成2个子节点,那么深度为 \(d\) 的树就会生成 \(2^d\) 个节点,两万个节点大概只有15层。所以生成树的时候一定要注意子节点的数量,在计算机术语中,我们管这个影响因素叫做Branching Factor。
所以我们还可以限制生成函数的深度,比如说10层以后自动退出,这样生成的树最多就只有 \(2^{10} = 1024\) 个节点了,这样即使以后长度和粗细是随机的,我们也不用但是会生成过量的节点了。
限制深度的写法如下:
private Node _build(Node node, int dep) {
cnt++;
// 终止条件:深度达到上限
if (dep == 10) return node;
// 子节点数量,在2左右正态分布
int numChild = (int)(rand() * 4);
for (int i = 0; i < numChild; i++) {
// 参数修改了
Node child = new Node(rand(MathHelper.Pi / 6f), node.size * 0.9f, node.length * rand() * 1.5f);
node.children.Add(_build(child, dep + 1));
}
return node;
}
当然,除了弹幕,我们还可以,快速生成树状物块:
代码如下:
private void _tile(Vector2 pos, Vector2 vel, Node node) {
Vector2 unit = (vel.ToRotation() + node.rad).ToRotationVector2();
for (float i = 0; i <= node.length * 4; i += 8f) {
Point p = (pos + unit * i).ToTileCoordinates();
Main.tile[p.X, p.Y] = new Tile();
Main.tile[p.X, p.Y].type = TileID.WoodBlock;
Main.tile[p.X, p.Y].active(true);
WorldGen.SquareTileFrame(p.X, p.Y);
}
foreach (var child in node.children) {
_tile(pos + unit * node.length * 4, unit, child);
}
}
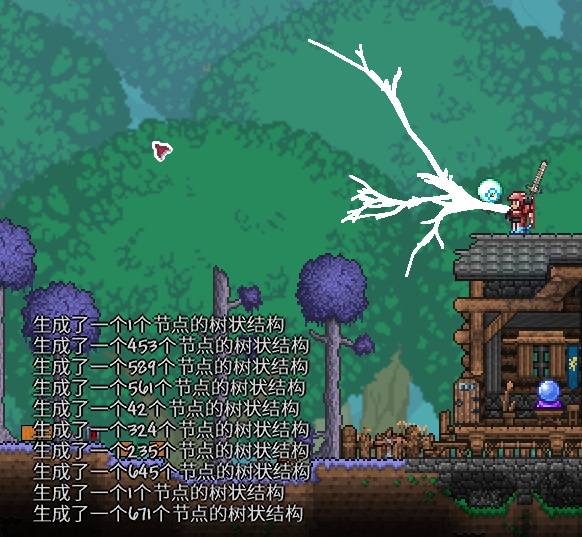
模拟闪电
在模拟自然物体之前,最好就是用眼睛先观察:
你观察到了什么?我可以告诉你我的发现:
- 闪电有一根主干,很粗,且角度变化也不大
- 闪电总体弯曲度不高,但是每一个小段方向变化的比较频繁,因此可能需要一条树枝上好几个节点进行方向变化
- 闪电很少出分叉,出的分叉粗细长短都远小于主干
- 分叉节点扭动比主干频繁
那么知道了这些,我们能怎样去优化生成树的算法呢?别急,我们一步步来:
因为有主干,所以我们需要一个方法去识别哪些个节点是主干,主干的粗细要比分支大,所以我们可以考虑给build加一个参数isMain,代表它是不是主干,并且对主干和非主干分别处理。同时因为分支不常出现,所以我们要修改分支生成的条件,这里我用非深度限制的生成函数来演示:
private Node _build(Node node, bool isMain) {
cnt++;
// 终止条件:树枝太细了,或者太短了
if (node.size < 0.1f || node.length < 1) return node;
float r = isMain ? MathHelper.Pi / 12f : MathHelper.Pi / 6f;
Node main = new Node(rand(r), node.size * 0.95f, node.length);
node.children.Add(_build(main, isMain));
// 只有较小的几率出分支
if (rand() > 0.85f) {
// 生成分支的时候长度变化不大,但是大小变化很大
Node child = new Node(rand(MathHelper.Pi / 3f), node.size * 0.5f, node.length);
node.children.Add(_build(child, false));
}
return node;
}
当然,要想让它更像闪电一点还需要调参的,这个参数并不好调,需要你不断的去完善自己的模型。所以多去尝试吧少年!
如果想让闪电有追踪效果,那么在建树的时候就需要把选中的NPC作为参数,然后每个节点都要尽可能靠近目标NPC,这个行为的具体实现方法很多,大家就自己尝试实现吧。
迷宫生成
树状结构除了用来模拟这些闪电什么的以外,还可以用来制作迷宫生成器。不管你信不信,迷宫其实就是一颗树。
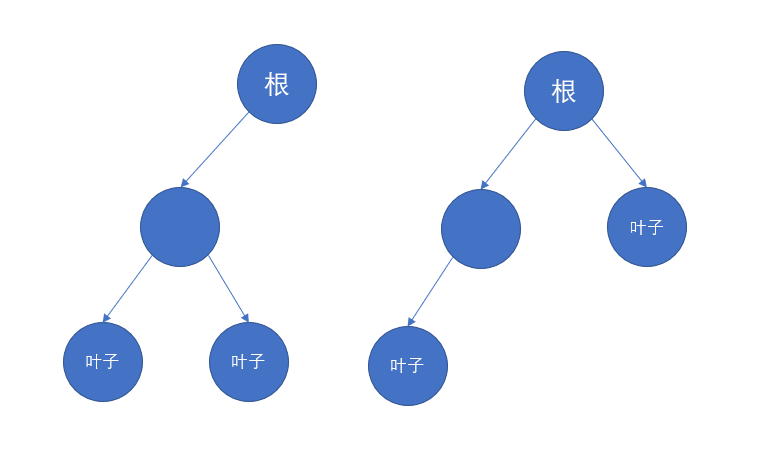
我们来看一下这张图吧:

图中的每一个箭头代表的就是迷宫中的路径,而树上的每一个节点代表的其实是一个单元格,但是每个单元格与父节点就构成了一条迷宫中的隧道。如果我们把树的边看做无向边,那么此时同一棵树上的任意两个节点都存在一条唯一的路径互相到达,这也就意味着,只要有两个单元格属于同一棵树,那么他们直接就能相互到达。
那么如果想让起点和终点能相互到达,只要构建一颗迷宫树就可以了,同时这样还可以让所有单元格直接互相到达。如果不想让所有单元格互相到达怎么办呢?这时候可以构建多颗树来覆盖所有单元格,这时候组成的图叫做森林。
本章我们只会讲构建一颗大迷宫树的算法,迷宫森林就留作作业。
结构设计
每个节点除了知道它是哪个单元格以外,我们还要知道它的是从父节点如何走到它的。具体来说,我们父节点可以有四个方向拓展:向左,向右,向上和向下。只有知道了父节点是如何扩展到子节点的,我们才能打通一条迷宫路径。
除此之外,为了定位单元格我们就只需要节点的坐标了。跟之前讲的差不多,我们仍然是先构建出树形结构:
private class Node {
public int dir, x, y;
public Node[] children = new Node[4];
public Node(int dir, int x, int y) {
this.dir = dir;
this.x = x;
this.y = y;
}
};
我们这次一个节点的子节点最多有4个,所以就使用大小为4的数组来存节点的引用。
注意到我们使用了一个int来代表方向,这个表示方法很重要,它简化了代码的复杂度。因为我们可以这样定义方向的x,y变化情况:
// 左右上下
private static int[] dx = { -1, 1, 0, 0 };
private static int[] dy = { 0, 0, -1, 1 };
那么(dx[0], dy[0]) = (-1, 0),就代表了向左走一格,以此类推,我们的4个方向全部包括在了这两个数组里面,这是实现上下左右行走问题的一个小技巧。
此外,我们还需要一个越界检查的check函数,对于DFS建树过程来说,我们不希望同一个点被访问多次(因为可能会死循环),所以我们还使用了一个二维数组vis来检测是否被访问过。以下就是构建好的基本环境,类内字段和方法
// 左右上下
private static int[] dx = { -1, 1, 0, 0 };
private static int[] dy = { 0, 0, -1, 1 };
private Node root;
private UnifiedRandom random;
private int maxX, maxY;
private bool[,] vis;
private int cnt;
public MazeTree(UnifiedRandom random) {
root = null;
this.random = random;
}
private bool check(int x, int y) {
return x >= 0 && x < maxX && y >= 0 && y < maxY && !vis[x, y];
}
建树
关于迷宫的建树方法其实有很多种,包括DFS建树,BFS建树,A*算法建树(随机最小权值法),以及其他杂七杂八的方法。这些方法的应用场景各不相同,所以没法说哪个更好,这里我们会介绍前三种。
DFS建树
DFS建树的好处就是代码简单,生成的迷宫分支比较少,很容易顺着走出去。我们的Build函数用于初始化搜索条件,vis数组置零等等:
public void Build(int x, int y) {
maxX = x;
maxY = y;
vis = new bool[x, y];
for (int i = 0; i < x; i++) {
for (int j = 0; j < y; j++)
vis[i, j] = false;
}
root = new Node(-1, 0, 0);
cnt = 0;
_build(root);
}
接下来就是_build这个递归函数了,我们要做的是对于每一个节点,以随机顺序挂上子节点,同时对子节点深度优先的递归。如果这个节点已经被访问或者出界了,我们要及时撤离这个节点,也就是返回一个null告知这个节点是空的。
private Node _build(Node node) {
// 不合法的节点就标记为空
if (!check(node.x, node.y)) return null;
vis[node.x, node.y] = true;
int[] dir = { 0, 1, 2, 3 };
// 打乱方向的搜索顺序,random shuffle函数,你值得拥有
for (int i = 3; i >= 0; i--) {
int j = random.Next(i + 1);
Terraria.Utils.Swap(ref dir[i], ref dir[j]);
}
// 按照打乱后的顺序进行深度优先建树
for (int i = 0; i < 4; i++) {
int d = dir[i];
Node nd = new Node(d, node.x + dx[d], node.y + dy[d]);
node.children[i] = _build(nd);
}
return node;
}
于是我们就完成了建树,简单吧?
但是这个问题的难点不在于建树,而在于如何根据树构建出真正的迷宫。这里我们可以建立一个模型:
也就是我们的迷宫路径挖掘模型,当我们有一条隧道挖向右边的时候,我们就要挖出黄色的隧道,当我们又有一条向下的路径的时候就要挖出绿色的路径。由于我们现在的单元格变成了3×3的,所以中间的部分就是可以通过的隧道了。
其实看着这幅图我们就能发现一些规律了,我们只需要每个单元格都填满,但是把中间的那一格挖空,然后往回挖两个小格即可。这里的往回是指往父节点到子节点的方向的反向,因为我们正处于子节点,我们记录了过来的方向信息,所以现在只需要反向挖回去即可。
说做就做,我们先定义一个用于初始化的Tile函数:
public void Tile(int x, int y) {
_tile(root, x, y);
}
然后就是最爱的递归构造环节了:
private void _tile(Node node, int x, int y) {
// 把3x3单元格填满
for (int i = -1; i <= 1; i++) {
for (int j = -1; j <= 1; j++) {
Main.tile[x + i, y + j] = new Tile {
type = TileID.WoodBlock,
};
Main.tile[x + i, y + j].active(true);
}
}
// 中间的清除掉
Main.tile[x, y] = new Tile();
// 如果不在根节点
if (node.dir != -1) {
// 获取方向的反向
int d = node.dir ^ 1;
// 挖空
for (int i = 1; i < 3; i++)
Main.tile[x + dx[d] * i, y + dy[d] * i] = new Tile();
}
// 顺着每个非空子节点继续构造迷宫
for (int i = 0; i < 4; i++) {
Node child = node.children[i];
if (child == null) continue;
// 因为单元格变成3x3,所以这里的坐标也要扩大三倍,总体迷宫范围扩大9倍
_tile(child, x + dx[child.dir] * 3, y + dy[child.dir] * 3);
}
}
反向函数我这里用了异或,也就是切换奇偶性,这样0会变成1,1会变成0,正好符合我们对方向的定义,就能很轻松的获取反向方向了。
我们只要把大小和目标迷宫区域的左上角坐标传给函数,就可以构建出一个迷宫了:
看看,是不是很符合dfs深度优先的特性?每个单元格都是联通的,而且目标路径很单调。
那么问题来了,3×3的迷宫人根本走不进去,这就不好玩了,如果这个单元格变成5×5的,墙壁还是1厚度,那么人就能走进去了,不过相应的打通隧道需要的代码也会多一些。因为中间要挖空的是3×3的空间了,不过同样也是挖掉两个空间,至于实现就自己想想喽。
BFS建树
BFS(广度优先搜索)建树会稍微复杂一点,因为我们需要使用优先队列进行随机化权值分配,由于C#的优先队列特别不好用,所以我这里提供了一个比较好用的优先队列类:
using System;
using System.Collections.Generic;
using System.Linq;
using System.Text;
using System.Threading.Tasks;
namespace TemplateMod2.Utils {
/// <summary>
/// 优先队列,使用小根堆实现,Pop,Push复杂度保证O(log n)
/// </summary>
/// <typeparam name="T"></typeparam>
public class PriorityQueue<T> where T : IComparable {
private T[] heap;
private int tot;
public PriorityQueue(int sz) {
tot = 0;
heap = new T[sz * 4];
}
public bool Empty { get => tot == 0; }
/// <summary>
/// 将元素放入小根堆
/// </summary>
/// <param name="val"></param>
public void Push(T val) {
heap[++tot] = val;
swim();
}
/// <summary>
/// 获取堆顶值
/// </summary>
public T Top => heap[1];
/// <summary>
/// 获取并弹出堆顶上的最小值
/// </summary>
/// <returns></returns>
public T Pop() {
T ret = heap[1];
swap(1, tot--);
sink();
return ret;
}
private void swap(int i, int j) {
T tmp = heap[i];
heap[i] = heap[j];
heap[j] = tmp;
}
private void swim() {
int k = tot;
while (k > 1 && heap[k >> 1].CompareTo(heap[k]) > 0) {
swap(k >> 1, k);
k >>= 1;
}
}
private void sink() {
int k = 1;
while ((k << 1) <= tot) {
int j = k << 1;
if (heap[k << 1].CompareTo(heap[k << 1 | 1]) > 0)
j++;
if (heap[k].CompareTo(heap[j]) <= 0) break;
swap(k, j);
k = j;
}
}
}
}
BFS建树的原理是这样,每次都取权值最小的那个节点进行路径生成,每次只会向4个方向生成路径。由于分配的权值随机,所以这个扩张顺序也会很随机,就这样生成了一个随机迷宫。
接下来我们就可以定义一个树上节点的大小关系了:
private class Node : IComparable {
public int dir, x, y, p;
public Node[] children = new Node[4];
public Node(int dir, int x, int y) {
this.dir = dir;
this.x = x;
this.y = y;
// 随机给一个权值
this.p = Main.rand.Next(10);
}
public int CompareTo(object obj) {
var node = (Node)obj;
return p.CompareTo(node.p);
}
};
之后我们直接在Build函数写就行:
public void Build(int x, int y) {
maxX = x;
maxY = y;
vis = new bool[x, y];
for (int i = 0; i < x; i++) {
for (int j = 0; j < y; j++) {
vis[i, j] = false;
}
}
root = new Node(-1, 0, 0, 0);
vis[0, 0] = true;
PriorityQueue<Node> Q = new PriorityQueue<Node>(x * y);
Q.Push(root);
while (!Q.Empty) {
var cur = Q.Top;
Q.Pop();
for (int i = 0; i < 4; i++) {
Node nd = new Node(i, cur.x + dx[i], cur.y + dy[i], random.Next(10000));
if (!check(nd.x, nd.y)) continue;
vis[nd.x, nd.y] = true;
cur.children[i] = nd;
Q.Push(nd);
}
}
}
这样我们就完成了一个随机BFS的生成树,构建迷宫的方式和之前的没有任何区别。
看,是不是和DFS构建出来的有所不同?










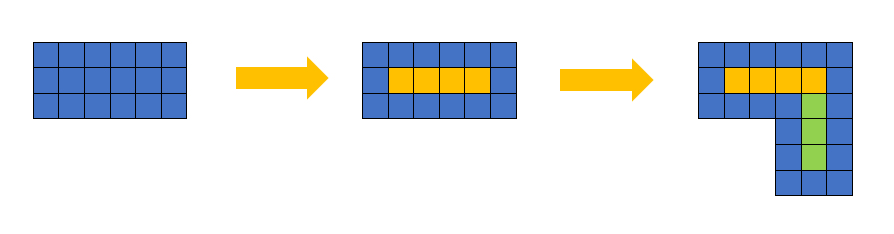


好,不愧是你
恶臭裙子,随缘更新。(其实已经逐渐变成算法教程了)
提问:为什么平时买西蓝花的时候不会卡呢?
看来地球OL处理器比较好
114514
h,bksn
好!
hbksn
好!我会了