问题简述
我们有时候会遇到这样的问题,在某处有一个敌人,它的速度为 \(\vec{v}\),此时你可以发射一个弹幕射向敌人。但是问题是,等你的弹幕移动到敌人刚才的位置的时候,敌人已经从原来的位置移动了一小段距离,那么你有很大几率无法打中敌人,尤其当敌人速度很快的时候。
如果你熟悉射击类或者动作类游戏,你肯定会想到去预判,可是怎么去预判才能有更大几率命中敌人呢?那么对于这个问题,我分成了三个类别考虑,我们先假设敌人和弹幕都是匀速直线运动,否则无法进行精准预判(难道要炼丹?)。
第一类问题,假设我们并不要求弹幕以某个速度或者角度运动,而是要求一定时间后击中目标。
第二类问题,很多时候武器的射速是固定的,所以我们只要求弹幕的射出速度固定,而不对角度和时间做要求。
第三类问题,比较不常见,这个武器的角度是固定的,但是不对速度和时间做限制。
在分析开始之前,我们先假设弹幕和敌人都是质点,这样方便计算。那么设玩家处于位置 \(p_1\) ,敌人处于位置 \(p_2\),且敌人的移动速度为 \(v_2\),玩家必须在时刻\(0\)的时候射出弹幕,弹幕的初速度为 \(v_1\)。那么由此可得方程
\[p_1+t\cdot v_1 = p_2+t\cdot v_2\]
这个方程将作为解决这个问题的主要方程。
限制时间
对于第一类问题来说,假设我们要在时刻 \(t_0 > 0\) 的时候击中目标,那我们简单的把 \(t\) 替换为 \(t_0\),于是解方程
\begin{align} p_1+t_0\cdot v_1 &= p_2+t_0\cdot v_2 \\ t_0\cdot v_1 &= p_2-p_1 + t_0\cdot v_2 \\ v_1&=\frac{p_2+t_0\cdot v_2-p_1}{t_0} \end{align}
那么对结果 \(v_1=\frac{p_2+t_0\cdot v_2-p_1}{t_0}\) 的通俗说法就是,先计算 \(p_2\) 移动 \(t_0\) 时间的位置,然后计算从玩家到目标位置的向量 \(\vec{u}\),此时\(\frac{\vec{u}}{t_0}\)就是发射弹幕的初始速度。
限制速度
第一类问题的解法确实非常简单,我们可以用这个公式准确的预判敌人位置,只不过限制时间的场景并不多,相反限制速度的第二类问题就比较常用,但是相应的预判难度也很大。
首先,由于 \(t\) 未知,该方程有两个未知数,所以我们无法求解?
方案1(强行解方程):
但是我们速度是限制的,我们先假设速度大小(速度向量的模长)恒定为 \(d\)。那么我们可以把 \(v_1\) 拆分成 \(v_{1,x}\),和 \(v_{1,y}\),我们现在需要确定的就是角度。其实这个问题里面的未知数角度和时间是相互依赖的,只要求出了任何一个就能马上求出另一个(共线的不算)。
根据向量的弧度公式,设角度为 \(\theta\) 我们有
\[\begin{cases} v_{1,x}=d\cos{\theta}\\ v_{1,y}=d\sin{\theta} \end{cases}\]
同样的,我们也把 \(p_1, p_2, v_2\) 拆成 \(x,y\) 分量,那么可得
\[
\left\{
\begin{aligned}
p_{1,x}+td\cos{\theta}&= p_{2,x}+tv_{2,x}\\
p_{1,y}+td\sin{\theta}&= p_{2,y}+tv_{2,y}
\end{aligned}
\right.
\]
看上去未知量更多了,不是吗?当然不是,未知量只有 \(\theta\) 和 \(t\),我们有两个方程两个未知数,那么此方程可解?
解\left\{
\begin{aligned}
td\cos{\theta}-tv_{2,x}&= p_{2,x}-p_{1,x}\\
td\sin{\theta}-tv_{2,y}&= p_{2,y}-p_{1,y}
\end{aligned}
\right.
\]
我们把 \(t\) 变到等式左边代换掉
\[
t(d\cos{\theta}-v_{2,x})= p_{2,x}-p_{1,x}\\t=\frac{p_{2,x}-p_{1,x}}{d\cos{\theta}-v_{2,x}}
\]
代回下面那个式子,得
\[\begin{aligned}
\frac{p_{2,x}-p_{1,x}}{d\cos{\theta}-v_{2,x}}(d\sin{\theta}-v_{2,y}) &= p_{2,y}-p_{1,y}\\
(p_{2,x}-p_{1,x})(d\sin{\theta}-v_{2,y}) &= (d\cos{\theta}-v_{2,x})(p_{2,y}-p_{1,y})\end{aligned}
\]
令 \[A=(p_{2,x}-p_{1,x}), B=(p_{2,y}-p_{1,y})\] 那么有:
\[\begin{aligned}Ad\sin{\theta}-Av_{2,y}&=Bd\cos{\theta}-Bv_{2,x}\\ Ad\sin{\theta}-Bd\cos{\theta}&=-Bv_{2,x}+Av_{2,y}\\ A\sin{\theta}-B\cos{\theta}&=\frac{Av_{2,y}-Bv_{2,x}}{d} \end{aligned}\]
这样左边是未知数,右边是个常数。然后众所周知 \(\sin(\alpha-\beta)=\sin\alpha\cos\beta-\cos\alpha\sin\beta\)(和差角公式)
我们把 \(\alpha\) 看作原式中的 \(\theta\) 那么有
\[\left\{\begin{aligned} \frac{B}{A} &= \frac{\sin(\beta)}{\cos(\beta)}\\ \frac{Av_{2,y}-Bv_{2,x}}{d} &= R\sin(\theta – \beta) \end{aligned}\right.\]
此时 \(\beta\) 即为 \(\tan^{-1}(\frac{B}{A})\),这个函数一定有解,所以角度 \(\beta\) 一定存在,这就像是一个向量的夹角了
而这里的 \(R\) 此时是三角形的缩放倍率,我们假设缩小 \(\frac{1}{R}\) 以后会变成单位向量,那么我们就可以求出
\[R=\sqrt{A^2+B^2}\] 我们重写原式为
\[\begin{aligned} \frac{Av_{2,y}-Bv_{2,x}}{d} &=\sqrt{A^2+B^2}\sin\left(\theta – \tan^{-1}(\frac{B}{A})\right)\\ \sin\left(\theta – \tan^{-1}(\frac{B}{A})\right) &= \frac{Av_{2,y}-Bv_{2,x}}{d\sqrt{A^2+B^2}}\\ \theta &= \sin^{-1}\left(\frac{Av_{2,y}-Bv_{2,x}}{d\sqrt{A^2+B^2}}\right)+\tan^{-1}(\frac{B}{A}) \end{aligned}\]
貌似我们就解决了这个问题,但是这个方程有时候无解,具体来说:
\(\sin^{-1}\) 这个函数的定义域是 \([-1, 1]\),所以如果 \(\frac{Av_{2,y}-Bv_{2,x}}{d\sqrt{A^2+B^2}}\) 脱离这个范围一定无解
我们再来看看 \(A\) 和 \(B\) 到底是什么
\[A=(p_{2,x}-p_{1,x}), B=(p_{2,y}-p_{1,y}) \\ (A, B) = p_2-p_1 = \vec{v}\]
\(\vec{v}\)也就是从玩家到敌人的向量,那么 \(Av_{2,y}-Bv_{2,x}\) 是什么呢?其实就是 \(\vec{v} \times \vec{v_2}\),他们两的cross product!
那么 \(\sqrt{A^2+B^2}\) 是?没错,就是 \(|\vec{v}|\) 啊哈,那\(\tan^{-1}(\frac{B}{A})\) 岂不是…… 向量 \(\vec{v}\) 的弧度?
舒服了舒服了!那么最终的公式可以写成
\[\theta = \sin^{-1}\left(\frac{(p_2-p_1)\times\vec{v_2}}{d|(p_2-p_1)|}\right) + rad(p_2-p_1)\]
嗯,非常可解,我们来验证一下是否正确吧
代码实现
private float crossProduct(Vector2 v1, Vector2 v2) {
return v1.X * v2.Y - v1.Y * v2.X;
}
public override bool Shoot(Player player, ref Vector2 position, ref float speedX, ref float speedY, ref int type, ref int damage, ref float knockBack) {
float maxDis = 1000f;
NPC target = null;
// 选取最近npc,如果target是null说明没有临近的敌人
foreach (var npc in Main.npc) {
if (npc.active && !npc.friendly && npc.value > 0 && !npc.dontTakeDamage) {
float dis = Vector2.Distance(npc.Center, position);
if (dis < maxDis) {
maxDis = dis;
target = npc;
}
}
}
if (target != null) {
// 获取从玩家到npc的向量
Vector2 plrToNPC = target.Center - position;
float speed = 12f;
float offset = plrToNPC.ToRotation();
// 这就是我们推出来的公式
float G = crossProduct(plrToNPC, target.velocity) / speed / plrToNPC.Length();
if (G > 1 || G < -1) {
Main.NewText("无法预判QAQ");
return true;
}
float realr = (float)(offset + Math.Asin(G));
Projectile.NewProjectile(position, realr.ToRotationVector2() * speed, type, 100, 5f, player.whoAmI);
return false;
} else {
return true;
}
}
但是这个方法……可解你个头哦,这个方程解起来就是噩梦好吧!要是加上其他运动轨迹(比如加速度)你给我解个看看?
方案2:迭代法
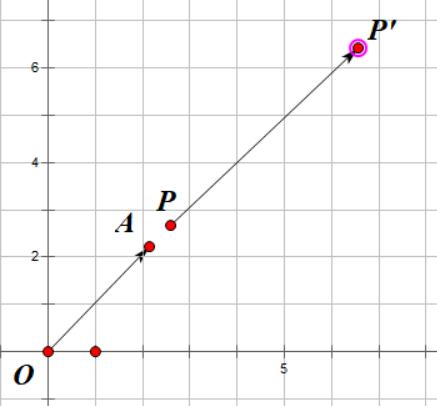
我们这么去想这个问题,假设我就是头铁,就是不预判直接瞄准射击!那么当我的弹幕到达敌人在时刻0的位置的时候,敌人在哪个位置?
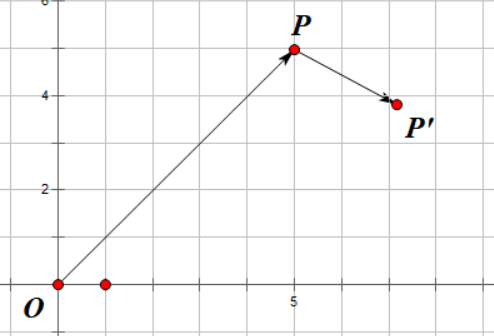
哦,我的子弹射到了点 \(P\) 但是敌人跑到了 \(P’\),我打不到它了QAQ。。。
不行,这次我就直接往点 \(P’\) 打,我就不信它还能躲掉!
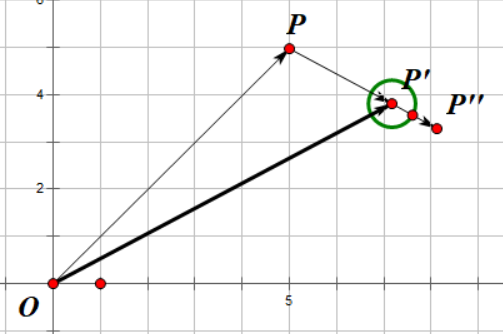
艹,还是被躲掉了,不过至少……比上次有进步,好,那我这次直接瞄准 \(P”\),你能躲掉?今天能把老子弹幕躲掉,我当场……
啊哈哈哈哈,还好靠着弹幕的碰撞体积打到了,不用吃屏幕了。那么这个故事告诉我们什么道理呢?(只要你打的够歪敌人就会撞上去)
就是一个原则:逼近。其实二分法就是利用了这种思想,每次排除掉一半的Search Space,从而达到不断逼近最终解的方式。而我们用的这个方法是比较符合直觉的,既然我第一次不够好,我就每次都修正自己的角度,既然我第一次没打到,我们就打个提前量,是不是这样?
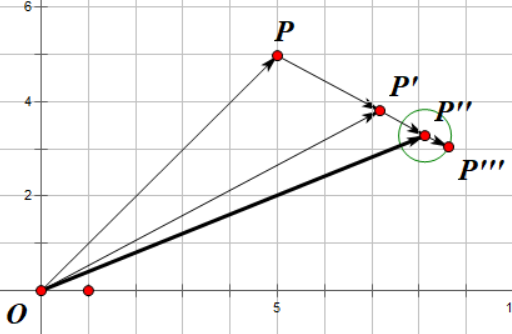
但是为什么我们能保证这个方法一定能逼近最终结果呢?事实上,我们保证不了,比如看这幅图
你觉得我们有办法打到敌人吗?唉,弹幕速度太慢了,再怎么追也追不上啊。如果我们真的按照之前的那个方法试下去的话,我们就会陷入死循环。我们人类可以判断出我们无法射中目标,但是电脑它不行啊,它只会盲目的尝试,丝毫不知道自己与正解背道而驰。
怎么办呢,我们可以设置一个迭代上限,那么这个不断尝试的过程在什么时候会终止呢?
- 当射中位置足够接近目标的预判位置,比如碰撞体积已经能够打到
- 当尝试了足够多次发现仍然无法接近正确的位置时
一般来说,10次迭代就能找到离敌人真实位置距离不超过 \(0.01\) 的位置,如果20次还没找到一个在精准度可接受范围内的目标发射向量,我们就可以放弃了。
那么我们就可以写出这样的代码:
private Vector2 GetShootVector(NPC npc, Vector2 pos, float speed) {
// 一开始我们假设往npc现在所处位置发射弹幕
Vector2 target = npc.Center - pos;
for (int i = 0; i < 20; i++) {
// 获取弹幕的飞行时间
float t = (target - pos).Length() / speed;
// 过了这么多时间以后npc到哪里了?
Vector2 npcPos = npc.Center + t * npc.velocity;
// 我们射到的位置是否距离npc最终位置足够近?
if (Vector2.Distance(target, npcPos) < 0.1f) {
Main.NewText("足够近");
// 足够近,我们直接返回这个发射向量
return (target - pos).ToRotation().ToRotationVector2() * speed;
}
// 不够近,我们把目标位置改动一下,进行下一次尝试
target = npcPos;
}
// 怎么样都不够近,算了放弃吧
return Vector2.Zero;
}
注意这里预判不成功会返回一个零向量,要注意特判。
这个方法的优点就是不用数学知识,缺点当然就是需要进行几十次迭代性能会差一点(说实话,10也太少了),且无法得出精确解。但是我们仔细想想,真的需要精确解吗?或者说,很多时候,我们能求出精确解吗?
所以这个方法是不是比第一个实用很多?
方案3:模拟轨迹+二分+迭代
那么我们再来考虑一下弹幕轨迹不是直线甚至非匀速的情况
比如说,我这弹幕是受重力下坠的,设 \(g = 0.3\) 那么弹幕射出来会是这样
弹幕击中怪物的方程可以这么表示(我们不会的去解它的,放心):
\[\vec{p_1}+t\vec{v_1}+0.5\vec{g}t^2 = \vec{p_2}+t\vec{v_2}\]
好嘛,未知数有个平方项,意味着解可能不止一个, 因为抛物线有上升状态和下降状态,为了简化模型,假设我们现在希望弹幕一定是在下落的过程中击中敌人(这无疑增加了难度,因为抛物线的轨迹你懂得……),我们还是限制初始发射速度。
但是在选择角度的时候我们还会遇到一个问题,就是对于同一个落点,可能有两个不同的角度都能到达,这里我们希望是高角度(大于45度),这样落点更精准,受高度影响更小。既然我们不可能去解方程,我们就要用另一种方法来确定我们的落点了,那就是模拟。
模拟是什么意思呢?就是我们先把未来弹幕发射后可能出现的轨迹先计算出来,然后判断我们选的角度是否能够击中敌人。虽然二次函数并不需要用模拟来判断落点,但是如果是三次,四次函数甚至不是多项式呢?这里我们就以受到只重力的二次函数弹幕为例,模拟一下发射出来的轨迹:
// 参数分别是,射出位置,射出速度,目标的位置和重力系数
private Tuple<float, int> GetHitPoint(Vector2 pos, Vector2 shootVec, Vector2 targetPos, float gravity) {
int t = 1;
while (true) {
pos += shootVec;
// 如果速度向下,就是下落状态,并且下落到与目标相同(或更低)的高度
// 越过了这个高度下落弹幕就没办法再击中敌人了,直接返回X坐标和所用时间
if (shootVec.Y > 0 && pos.Y > targetPos.Y)
return new Tuple<float, int>(pos.X, t);
// 模拟重力作用
shootVec.Y += gravity;
t++;
}
}
接下来我们就根据这个落点X坐标就可以判断我们角度是大了还是小了。对于45度以上的角度来说,越靠近45度角肯定X坐标越远,反之落点X坐标越近,那么我们就可以利用这个性质进行二分搜索。如果不会二分可以看以前的博客。
于是我们的预判策略就变成:
- 模拟轨迹计算出某个角度发射弹幕的实际落点
- 二分查找搜索出到达某个固定落点所需要的角度,和时间
- 利用之前的迭代法找到预判落点的位置以及所需的发射角度
那么代码如下
// 获取到达固定点target所需的发射向量以及时间
private Tuple<Vector2, int> GetShootVec(Vector2 pos, Vector2 target, float speed, float gravity) {
// 二分法的范围包括了左右两边的弧度,要注意一下
float L = -MathHelper.PiOver2, R = -MathHelper.PiOver4;
Tuple<Vector2, int> ans = new Tuple<Vector2, int>(Vector2.Zero, 0);
// 精度足够我们就停止
while (R - L > 0.001f) {
float mid = (L + R) / 2;
Tuple<float, int> tmp = GetHitPoint(pos, mid.ToRotationVector2() * speed, target, gravity);
// 如果X坐标在目标左边说明我们要降低角度,反之增加
if (tmp.Item1 < target.X) {
L = mid;
} else {
R = mid;
}
ans = new Tuple<Vector2, int>(mid.ToRotationVector2() * speed, tmp.Item2);
}
return ans;
}
// 获取预判向量
private Vector2 GetPredictVec(Vector2 pos, NPC npc, float speed, float gravity) {
// 一开始我们假设往npc现在所处位置发射弹幕
Vector2 target = npc.Center - pos;
for (int i = 0; i < 20; i++) {
// 获取弹幕的飞行时间和射出速度
Tuple<Vector2, int> info = GetShootVec(pos, target, speed, gravity);
// 过了这么多时间以后npc到哪里了?
Vector2 npcPos = npc.Center + info.Item2 * npc.velocity;
// 我们射到的位置是否距离npc最终位置足够近?
if (Vector2.Distance(target, npcPos) < 0.1f) {
Main.NewText($"足够近 {info.Item2} {info.Item1}");
// 足够近,我们直接返回这个发射向量
return info.Item1;
}
// 不够近,我们把目标位置改动一下,进行下一次尝试
target = npcPos;
}
// 怎么样都不够近,算了放弃吧
return Vector2.Zero;
}
有几点需要注意,第一,TR世界坐标是X,Y倒过来的,所以我们的弧度也得取负数(代码很多地方都反过来了)。第二,由于我只考虑了45度到90度的场景,没有考虑90度到135度的场景,所以只能朝右边发射,但是你可以用判断怪物在玩家左右的方法让这个算法也支持向左发射。
第三,由于抛物线能到达的距离有限,所以很有可能无论无何都打不到敌人,这时候该如何判断呢?
第四,这个算法的时间复杂度大概是 \(O(Cn\log{W})\) 其中 \(C\) 是迭代次数的影响因素,\(W\) 是二分时的角度范围,这里大概是弧度范围除以精度,\(n\) 是模拟弹幕轨迹的次数。由此看来,这个算法时间复杂度还是挺高的,但是事实上,\(C\) 的影响因素可以被消去,因为迭代和二分可以一起进行,但是代码也会变复杂。
还好, \(O(Cn\log{W})\) 这个复杂度电脑可以接受,就是不要进行太多次就好了。
我们看看效果吧
总结一下,对于非线性弹道,精准预判是极其困难的,不论是对人还是对电脑,我们只能牺牲电脑的运行速度从而避免推公式。但是话又说回来,电脑的出现不就是为了帮助人类进行重复性的计算吗?
限制角度
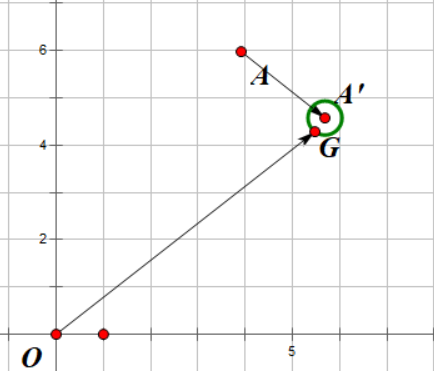
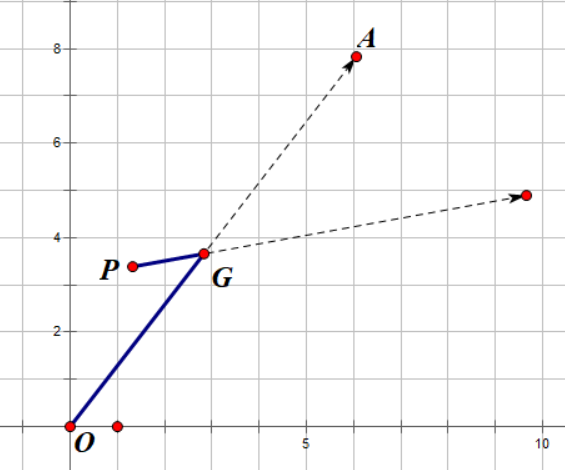
限制角度的话,能击中的范围就更小了,因为显然需要时间为负数的目标点我们不可能击中,在这种情况下,我们只需要判断两直线交点。如果没有交点显然不可能预判,否则我们判断相交线段的长度之比,就是目标速度了。如果速度是负数那么显然就不是原来的角度了,因此无法预判。
此时 \( |\overrightarrow{PG}| \) 与 \( |\overrightarrow{OG}| \) 的比值就是敌人速度与弹幕速度的比值了。
(写的好累啊,留点坑以后补上吧)




我来了!
……我傻了
你看这个式子多美啊(迫真)
预判的事明明应该是玩家做【】