第一版。
浅绿色代表进阶内容,浅蓝色代表附加信息,浅红色代表需要注意的内容。
需要知道的概念:函数、实数。不要被公式吓到!公式大部分都没用,如果想要看实现代码,请直接点击下方的按钮
1 最基础的随机分布——均匀分布
在很多地方都要用到随机数的生成。而最基础的随机数,就是计算机为我们(用时间为种子)生成的(伪)随机数。这样子生成的随机数听从均匀分布(Uniform Distribution)。
那到底什么是分布?简单的来说,分布,这里指概率密度函数pdf,就是一个(数学意义上的)函数\(\newcommand{\R}{\mathbb{R}} \renewcommand{\P}{\mathbb{P}} \newcommand{\E}{\mathbb{E}} \renewcommand{\bar}[1]{\overline{#1}} f: \R \to \R\),并且从这里来的随机数,它指的是:\(x\)的相对概率(相对于从同一个分布生成出的其它随机数而言)是\(f(x)\)。函数哪里高,随机到那个数的概率就大,反之亦然。
进阶:并且,如果用\(\P(A)\)代表\(A\)发生的概率(概率是从0到1的一个实数),假设某个不知道的随机数\(X\)来源于\(f\),那么$$\P ( X \leq x ) = \int_{-\infty}^x f(m) dm, $$ 并且记作\(F(x) := \P (X \leq x)\)。我们称这个函数为累积分布函数CDF。也就是说,给定一个数\(x\),在这个分布下,你随机到另一个你还没随机的数\(X\)比\(x\)小的概率是\(F(x)\)。
这样一来,我们发现,由于数(假设是实数)是无穷的,我们确切的随机到某一个数(比如0.5)的概率一定是0 (为什么?请你自己想一想) !所以我们只能对于一个范围进行预测,预测随机到的数在这个范围内的概率。
进阶:如果这个范围是\((a, b)\),那么概率应该是\(\P(X \in (a, b)) = F(b) – F(a)\)。
定理1:简单的来说,PDF函数纵轴\(f(x)\)代表了随机到某个数\(x\)的可能性,函数值越大,随机到那个数的可能性就越高。由此可知,PDF一定是正的(因为概率不能是负数),并且下面的区域的面积之和一定要是1(因为不管怎么随机,随机到的数的概率全部加起来肯定是100%)。
注意:我们概率使用的是闭区间0到1,即\([0,1]\)之间的一个数,如果你习惯使用百分比,那请你把这个数乘以100再加上一个百分号即可。例如概率\(0.5 = 50\%\)。
均匀分布
现在可以来讲讲均匀分布。首先,计算机为我们生成的数是从0到1之间的一个数。这是一个均匀分布。之所以均匀,是因为它的PDF \(f\) 是常数,当然只是在\((0, 1)\)上是常数,在其它情况下都是0。我们能计算出这个常数吗?(使用定理1?)
解答:因为我们只在0到1之间生成,所以在此之外的所有区域PDF函数的值都为0(为什么?因为pdf函数的值代表了随机到那个数的相对概率,在这里一定是0)。然后,既然是一个常数,那令它为\(c\),即\(f(x) = c, x \in (0,1)\)。并且,我们知道函数下面的面积之和是1,所以我们可以得到一个方程(注意这个面积区域是一个长方形) $$ c \cdot (1 – 0) = 1 $$ 解得,\(c = 1\)。
更通用地,在区间\((a, b)\)上的均匀分布,记作\(\text{Unif}(a, b)\),的pdf是 $$f(x) = \begin{cases} \displaystyle \frac{1}{b-a} & a < x < b \\ \\ 0 & 其它 \end{cases}$$
这里有关开区间还是闭区间的讨论是不必要的。刚才说了,取到任意一个数的概率都是0,所以取到\(a\)或\(b\)的概率也是0,不影响pdf!
在C#中,我们很容易生成这样的随机数,而这也是基础中的基础。
var rand = new Random(); double rv = rand.NextDouble();
顺便一说,我也会放出提到的分布的pdf与cdf的图像以供参考。
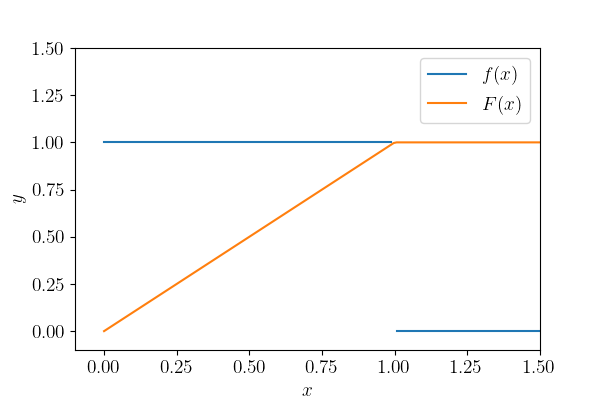
于是,我们很容易能得到,想要获得\(\text{Unif}(a, b)\)的变量,只需先从\(\text{Unif}(0, 1)\)中生成变量\(x\),然后执行 $$ y = x (b – a) + a$$ 那么这里的\(y\)就是\(\text{Unif}(a, b)\)的变量。同样的,如果要生成从a到b-1的整数变量,那么只要将\(y\)变成整数(去尾法)就行了((int) y)!是不是很简单?
当然,C#提供了生成从a到b-1的整数的方法。详细可以参阅Random.Next方法。
2 正态分布
我们现在不会满足于只能生成概率均相同的均匀分布。现在引入一个非常非常非常非常重要的分布——正态分布,或者高斯分布。首先,正态分布的pdf非常复杂,这里先不说。我们需要首先关注我们日常统计数据中十分常用的两个量:平均值\(\mu\)[mu]与标准差\(\sigma\)[sigma](这里一般使用它的平方,也就是方差\(\sigma^2\))。
平均值
平均值是非常重要的概念。在一组数据\(x_1, \dots, x_n\)中,数据(样本)的平均值的计算方法是 $$ \bar X_n = \bar \mu = \sum_{i = 1}^n x_i = x_1 + \cdots + x_n.$$ 虽然样本均值是很简单的概念,大家平时考试也十分关注平均分,但是对于一个随机分布(例如一个年级的考试成绩)来说,是极其重要的,也是规定某个分布pdf的形状的因素之一(另一个就是方差)。它告诉了我们随机变量可能会集中出现在哪里。
对于一个连续的分布(pdf)而言,也有它的均值,即这整个分布的均值。想象从一个分布中生成无穷多个变量,那这无穷多个变量的均值,就是这个分布的均值。
我们称其为从分布\(F\)中产生随机变量\(X\)的期望,或数学期望,定义为 $$ \mu = \E[X] = \int_\R x f(x) dx. $$ 根据大数定理,当数据量足够大的时候,数据的均值会逐渐趋向于数据的随机变量的期望,即\(\lim_{n \to \infty} \bar X_n = \mu\)。
你可能发现了,上面带横杠的表示样本(数据)的性质,而不带横杠的表示了随机变量(分布)的性质。
方差
方差就是一个相对复杂的概念,但是是另一个pdf的决定因素。方差表示了数据整体对于平均值的偏移(更准确的来说是分散)情况。即,如果数据非常分散(例如均匀分布),那么方差会大;如果数据非常集中于平均值,那么方差会小。接下来是样本方差的定义:$$ \bar \sigma^2 = \frac{1}{n – 1} \sum_{i = 1}^n (x_i – \bar \mu)^2, $$其中\(\bar \mu\)是数据的均值。样本标准差即为\(\bar \sigma\)。
接下来就是一个随机变量\(X\)的方差。定义如下:$$\newcommand{\Var}{\mathrm{Var}} \sigma^2 = \Var(X) = \int_\R (x – \mu)^2 f(x) dx $$ 聪明的同学可能已经看出来了,我们又有 定理2:$$ \Var (X) = \E [(X – \E [X])^2] = \E[X^2] – \E [X]^2$$
均值与方差的意义
这里,我将生成有不同均值与方差的正态分布变量,并用直方图表示出来。我一共生成了两次10000个正态分布变量,如下图所示。
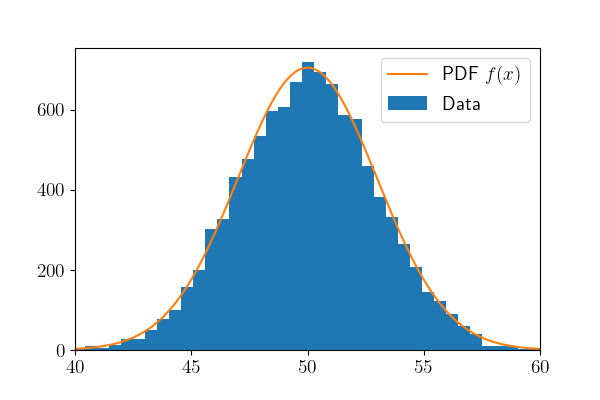
\(\mu = 50, \sigma^2 = 3\)
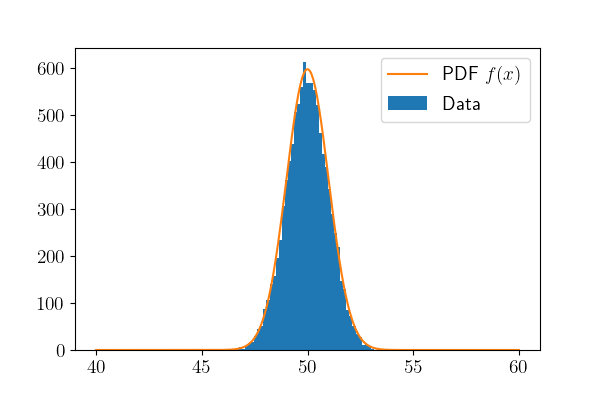
\(\mu = 50, \sigma^2 = 1\)
我们可以明显看到,方差越大,数据越分散。并且均值规定了数据集中的位置,在这里是50。黄色的线表示了它的pdf,当然只是作为参考,实际的pdf没有那么高,因为这里纵轴是每个区间数据的个数。
正态分布
现在我们可以使用我们学到的知识来看正态分布了。正态分布是极其重要的分布,它的CDF十分复杂,无法用基本函数表达,但是pdf可以用基本函数表达出来。我们把正态分布记作\(\mathcal{N} (\mu, \sigma^2)\)。下面是它的pdf:$$ f(x; \mu, \sigma^2) = \frac{1}{\sqrt{2\pi}\sigma} \exp \left (-\frac{(x-\mu)^2}{2\sigma^2} \right ), $$ 其中\(\exp\)是指数函数。虽然也很复杂,但是具体使用的话会很简单,我们先来看它的图像。
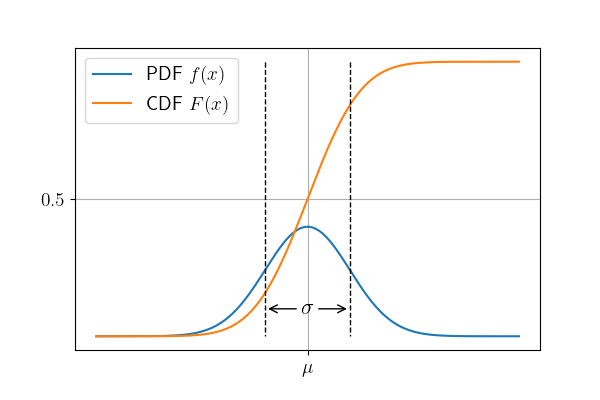
我们能发现,它的pdf关于\(\mu\)中心对称,也就是说,你抽到的数比\(\mu\)小的概率和比它大的概率是一样的,并且,距离\(\mu\)越大的数抽到的概率越小。抽到在\(\mu \pm 3\sigma\)之外的数的概率只有0.27%!这样的随机会让我们对生成的随机数有所控制,或有更多选择。
应用场景:通过这样生成出的随机数,我们可以不经处理而直接使用。例如,我要生成怪物根据等级\(l\)的攻击力\(a\),并且我想要攻击力是随机的,随等级提高而提高。那么,在创建某个等级的怪物时,我们可以从正态分布抽样\(a \sim \mathcal N (ml, 2)\),这样攻击力便会有均值\(ml\)和方差2(\(m\)是我们自己定义的常数),我们也就能知道大致在什么范围(也有可能会很大很小,但概率极低)。
标准正态分布
现在,我们知道了正态分布之后,它有一个特殊形态,称作标准正态分布,也就是当\(\mu = 0, \sigma^2 = 1\)的时候的正态分布,即\(\mathcal N (0, 1)\)。它之所以很重要,是因为一个我们不需要知道的定理(见定理3)。
定理3 中心极限定理:
若有数据\(X_1, \dots, X_n\),定义样本均值\(\bar X_n = \frac{X_1 + \cdots + X_n}{n}\),那么有 $$\frac{\bar X_n – \mu}{\sigma / \sqrt{n}} \overset{d}{ \longrightarrow } \mathcal N (0, 1). $$ 即,如果数据从某个具有均值\(\mu\)与方差\(\sigma^2\)的分布而来,那么他们的平均值将趋向于\(\mathcal N (\mu, \frac{\sigma^2}{n})\)。
正态分布的随机变量的生成
现在我们要开始说应该如何生成正态分布的随机变量。首先,你当然可以使用别人写的库,然后调用函数,但这是一个非常重量级的方法,因为如果你只需要生成比如正态分布的变量,而别人的数学库里有99%的东西你用不到,那这会令你的mod变得很臃肿。所以,我们其实有很方便的方法来生成这些变量,我们可以自己写代码来生成。
而首先,我们需要先知道怎么生成标准正态分布随机变量。生成标准正态分布变量的方法叫做 Box-Muller 算法。算法具体如下。
- 生成\(U_0, V_0 \sim \mathrm{Unif}(0, 1)\)。使用计算机内置的random即可,数据类型最好是
double。 - 计算\(U = -2 \ln U_0\)和\(V = 2\pi V_0\)。
- 获得一组标准正态分布的随机变量\(\displaystyle (X, Y) =( \sqrt{U} \cos V, \sqrt U \sin V)\)。
代码如下。
public static double StdGaussian()
{
var rand = new Random();
double u = -2 * Math.Log(rand.NextDouble());
double v = 2 * Math.PI * rand.NextDouble();
return Math.Sqrt(u) * Math.Cos(v);
}
接下来,我们就要用到正态分布的性质:$$\frac{X-\mu}{\sigma} \sim \mathcal{N}(0,1)$$ 来生成给定参数的正态分布随机变量。即,如果能得到一个标准正态分布的随机变量\(Z\),那么\(\sigma Z + \mu\)就是一个\(\mathcal N (\mu, \sigma^2)\)分布的随机变量。所以,代码如下。
public static double Gaussian(double mu, double sigma)
{
return StdGaussian() * sigma + mu;
}
3 更多分布以及更多抽样方法
指数分布
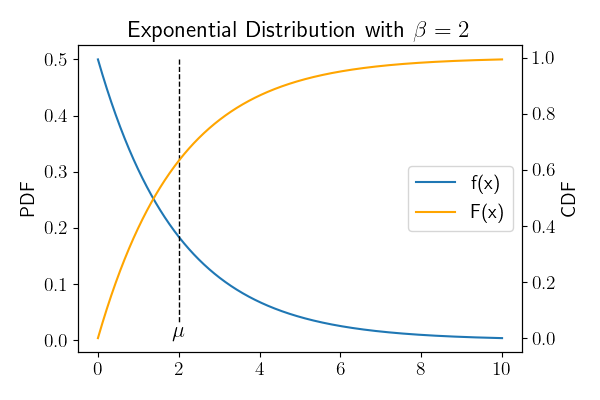
| $$ f(x) = \frac{1}{\beta} \exp \left (-\frac{x}{\beta} \right) $$ | |
| CDF | $$ F(x) = 1 – \exp \left (-\frac{x}{\beta} \right ) $$ |
| 均值 | $$\mu = \beta$$ |
| 方差 | $$ \sigma^2 = \beta^2 $$ |
这里可以看到,指数分布,抽到比平均值越大的数的概率是指数递减的。这也是一个很常用在建模上的分布。它一般用来表示独立随机事件发生的时间间隔,比如旅客进入机场的时间间隔、打进客服中心电话的时间间隔等。
指数分布有一个非常好的性质,称为无记忆性:如果一个随机变量\(T\)呈指数分布,那么它的条件概率遵循:$$ \P(T > s + t | T > t) = \P ( T > s) $$ 拿客服接电话举例子。如果用\(T\)表示第\(n\)分钟后客服接到一个电话,那么,他在第\(n + s\)分钟接到电话的概率,和他在第\(s\)分钟接到电话的概率是相等的。这看起来好像是没有意义的例子,但是这就代表了指数分布的随机性的特点,即事件的发生并不影响后续事件发生的概率。
逆抽样算法
逆抽样是一个生成随机变量的算法。根据所需要的CDF,生成符合该CDF的随机变量。如果给定一个可逆的CDF,即它单调递增,\(f(x)>0\),那么我们就能使用逆抽样算法。算法如下。
- 首先抽取\(U \sim \text{Unif} (0, 1)\)。
- 计算\(X = F^{-1}(U)\)。得到的\(X\)即是我们想要的符合CDF\(F(x)\)的随机变量。
证明:令\(U \sim \mathrm{Unif}(0, 1)\)。那么,$$ \P(F^{-1}(U) \leq t) = \P( U \leq F(t)) = F(t), \tag{1} $$ 因为\(U\)的cdf是\(F_U(u) = u\),然后\(\P(U \leq F(t)) = F_U(F(t)) = F(t)\)。于是,通过等式\((1)\),我们得出结论:\(F^{-1}(U)\)与\(X \sim F(x)\)是一样的(有同一个cdf\(F(x)\))。□
懵 逼
看不懂可以提问,,
表示看懂了,惊了
裙子NB!
这是Rebuild大佬写的…吧(
好!
这个可以做什么?上学期刚刚学了概率论还是记得一点的
没怎么看得懂。。。。。
太难了。。。。。